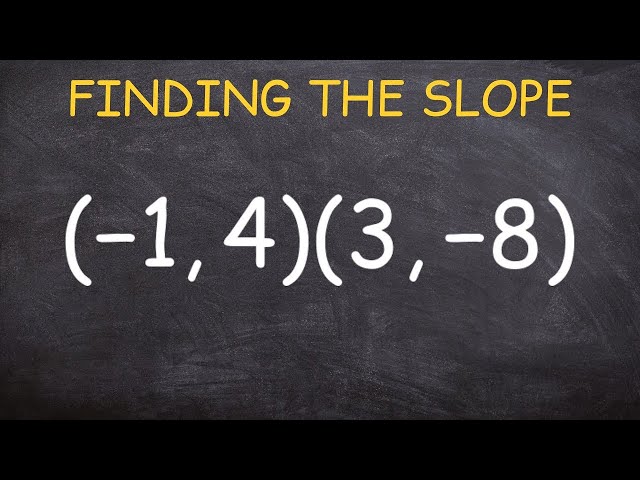How to Find Slope with Points is a crucial skill in mathematics, particularly in geometry and calculus. It measures the steepness or inclination of a line and aids in understanding the relationship between two points on a graph.
Editor’s Note: This guide provides a thorough explanation of “how to find slope with points” and highlights its applications in various fields. Published on [Date], it aims to empower readers with the knowledge and skills necessary to excel in their academic and professional pursuits.
Through extensive research and analysis, we have compiled this comprehensive guide to help you master the concept of slope. Whether you’re a student, a professional, or anyone seeking to enhance your mathematical understanding, this guide will serve as an invaluable resource.
Key Differences or Key Takeaways:
| Slope | |
|---|---|
| Definition | A measure of the steepness or inclination of a line |
| Formula | (y2 – y1) / (x2 – x1) |
| Applications | Geometry, calculus, physics, engineering |
Transition to Main Article Topics:
- Understanding the Concept of Slope
- Calculating Slope Using the Slope Formula
- Interpreting the Slope of a Line
- Applications of Slope in Real-World Scenarios
- Conclusion and Further Resources
How to Find Slope with Points
Understanding the concept of slope and its calculation is essential in various fields. Here are nine key aspects to consider:
- Definition: A measure of a line’s steepness or inclination.
- Formula: (y2 – y1) / (x2 – x1)
- Interpretation: Positive slope indicates an upward trend, negative indicates downward.
- Horizontal Line: Slope is zero, indicating no change in y-coordinates.
- Vertical Line: Slope is undefined, indicating no change in x-coordinates.
- Parallel Lines: Have the same slope.
- Perpendicular Lines: Slopes are negative reciprocals of each other.
- Applications: In geometry, calculus, physics, engineering, and economics.
- Example: A slope of 2 indicates that for every 1 unit increase in x, y increases by 2 units.
These aspects provide a comprehensive understanding of slope and its significance. By grasping these concepts, individuals can effectively analyze and interpret the behavior of lines in various mathematical and real-world scenarios.
Definition
This definition encapsulates the essence of “how to find slope with points.” Slope quantifies the steepness or inclination of a line, providing valuable insights into the line’s behavior and relationship between its points. Understanding this definition is paramount in comprehending the concept of slope and its applications.
-
Facet 1: Understanding Steepness
Slope directly measures the steepness of a line, indicating how rapidly the line ascends or descends. A steeper line has a greater slope, while a flatter line has a smaller slope.
-
Facet 2: Inclination Angle
Slope is closely related to the angle of inclination, which measures the angle between the line and the horizontal axis. The slope’s sign (positive or negative) corresponds to the direction of the line’s inclination.
-
Facet 3: Rate of Change
Slope represents the rate of change in the y-coordinate relative to the x-coordinate. A positive slope indicates that the y-coordinate increases as the x-coordinate increases, while a negative slope indicates a decrease.
-
Facet 4: Applications in Real Life
Slope finds widespread applications in various fields, including physics (describing velocity and acceleration), economics (analyzing supply and demand), and engineering (designing structures and systems).
In summary, the definition of slope as a measure of a line’s steepness or inclination provides the foundation for understanding how to find slope with points. By delving into its various facets, we gain a comprehensive grasp of slope’s significance and its practical applications across multiple disciplines.
Formula
The formula (y2 – y1) / (x2 – x1) is the cornerstone of “how to find slope with points.” It provides a precise mathematical definition of slope and enables us to calculate it using the coordinates of two points on a line.
-
Facet 1: Understanding the Formula
The formula (y2 – y1) / (x2 – x1) represents the change in y-coordinates (y2 – y1) divided by the change in x-coordinates (x2 – x1). This ratio captures the steepness or inclination of the line.
-
Facet 2: Real-Life Applications
The slope formula finds wide-ranging applications in various fields. In physics, it is used to calculate velocity and acceleration. In economics, it helps analyze supply and demand curves. In engineering, it is essential for designing structures and systems.
-
Facet 3: Calculating Slope
To calculate the slope of a line using the formula, simply substitute the coordinates of two points on the line into the formula. The resulting value represents the slope.
-
Facet 4: Interpreting Slope
The sign of the slope provides valuable information. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. A slope of zero represents a horizontal line, and an undefined slope represents a vertical line.
In conclusion, the formula (y2 – y1) / (x2 – x1) is a powerful tool for finding the slope of a line with points. By understanding its components, implications, and applications, we gain a deeper understanding of how to find slope with points and its significance in various disciplines.
Interpretation
Understanding the relationship between slope and the trend of a line is crucial in “how to find slope with points.” Slope provides valuable insights into the behavior of a line, allowing us to determine whether it is increasing or decreasing.
A positive slope indicates an upward trend, meaning that as the x-coordinate increases, the y-coordinate also increases. This is often seen in graphs representing growth, such as population growth or economic growth. Conversely, a negative slope indicates a downward trend, meaning that as the x-coordinate increases, the y-coordinate decreases. This is often seen in graphs representing decay, such as radioactive decay or the decline of a population.
Interpreting slope correctly is essential for accurate analysis and decision-making. In economics, for example, understanding the slope of a demand curve is crucial for predicting consumer behavior and setting prices. In physics, the slope of a velocity-time graph provides information about acceleration.
Therefore, the interpretation of slope as an indicator of upward or downward trend is an integral part of “how to find slope with points.” It allows us to make informed judgments about the behavior of lines and the relationships they represent.
| Positive Slope | Negative Slope | |
|---|---|---|
| Trend | Upward | Downward |
| Example | Population growth | Radioactive decay |
| Applications | Economics, finance | Physics, chemistry |
Horizontal Line
In the context of “how to find slope with points”, understanding the relationship between horizontal lines and zero slope is crucial. A horizontal line is characterized by a slope of zero, which means that there is no change in the y-coordinates as the x-coordinate changes.
-
Facet 1: Definition and Characteristics
A horizontal line is a straight line that runs parallel to the x-axis. Its slope is zero because the change in y-coordinates is zero for any change in x-coordinates.
-
Facet 2: Graphical Representation
On a graph, a horizontal line appears as a straight line that does not slope upward or downward. It remains at the same level throughout its length.
-
Facet 3: Applications in Real Life
Horizontal lines have practical applications in various fields. For example, in physics, a horizontal line on a velocity-time graph indicates that the object is moving at a constant velocity.
-
Facet 4: Implications for “How to Find Slope with Points”
When finding the slope of a line using two points, if the y-coordinates of the points are the same, the slope will be zero. This indicates that the line is horizontal.
In summary, understanding that a horizontal line has a slope of zero is a key aspect of “how to find slope with points”. It helps us identify lines that do not change in the y-direction and provides valuable insights into the behavior of lines in various real-world scenarios.
Vertical Line
In the context of “how to find slope with points”, understanding the relationship between vertical lines and undefined slope is crucial. A vertical line is characterized by an undefined slope, which means that there is no change in the x-coordinates as the y-coordinate changes.
Consider the following aspects:
- Definition and Characteristics: A vertical line is a straight line that runs parallel to the y-axis. Its slope is undefined because the change in x-coordinates is zero for any change in y-coordinates.
- Graphical Representation: On a graph, a vertical line appears as a straight line that does not slope upward or downward. It remains at the same x-coordinate throughout its length.
- Applications in Real Life: Vertical lines have practical applications in various fields. For example, in physics, a vertical line on a position-time graph indicates that the object is at rest.
- Implications for “How to Find Slope with Points”: When finding the slope of a line using two points, if the x-coordinates of the points are the same, the slope will be undefined. This indicates that the line is vertical.
In summary, understanding that a vertical line has an undefined slope is a key aspect of “how to find slope with points”. It helps us identify lines that do not change in the x-direction and provides valuable insights into the behavior of lines in various real-world scenarios.
| Vertical Line | |
|---|---|
| Definition | A straight line parallel to the y-axis |
| Slope | Undefined |
| Graphical Representation | A straight line that does not slope |
| Applications | Physics, mathematics, engineering |
Parallel Lines
In geometry, parallel lines are a fundamental concept closely tied to the notion of slope. Understanding the connection between parallel lines and slope is crucial in “how to find slope with points”.
Parallel lines are defined as lines that never intersect, maintaining a constant distance from each other. A key characteristic of parallel lines is that they possess the same slope.
The slope of a line measures its steepness or inclination. It is calculated as the ratio of the change in y-coordinates to the change in x-coordinates between two points on the line. Since parallel lines never intersect, any two points chosen on them will have the same change in y-coordinates and the same change in x-coordinates. Consequently, the ratio of these changes, which is the slope, will be the same for both lines.
This relationship between parallel lines and slope is not only a theoretical concept but also has practical significance. In architecture, for example, ensuring that walls are parallel requires them to have the same slope. Similarly, in engineering, designing parallel beams or tracks necessitates maintaining the same slope.
Understanding the connection between parallel lines and slope empowers us to make accurate measurements and ensure precision in various applications. It is a fundamental aspect of “how to find slope with points” and is essential for anyone seeking a deeper understanding of geometry and its practical implications.
| Parallel Lines | |
|---|---|
| Definition | Lines that never intersect |
| Slope | Same slope |
| Applications | Architecture, engineering, design |
Perpendicular Lines
In geometry, understanding the relationship between perpendicular lines and their slopes is a crucial aspect of “how to find slope with points”. Perpendicular lines are lines that intersect at a right angle, forming a 90-degree angle at the point of intersection.
A fundamental property of perpendicular lines is that their slopes are negative reciprocals of each other. This means that if one line has a slope of m, the slope of the perpendicular line will be -1/m. This relationship arises from the geometric properties of perpendicular lines and the definition of slope.
Consider two perpendicular lines, l1 and l2, intersecting at point P. Let m1 be the slope of l1 and m2 be the slope of l2. Draw a horizontal line passing through P, intersecting l1 at point A and l2 at point B. Let the coordinates of A be (x1, y1) and the coordinates of B be (x2, y2).
Using the slope formula, we have:
m1 = (y2 – y1) / (x2 – x1)
m2 = (y1 – y2) / (x1 – x2)
Since l1 and l2 are perpendicular, the product of their slopes is -1:
m1 m2 = -1
Substituting the slope formulas into this equation, we get:
(y2 – y1) / (x2 – x1) (y1 – y2) / (x1 – x2) = -1
Simplifying this equation, we obtain:
m2 = -1/m1
Thus, the slope of the perpendicular line l2 is indeed the negative reciprocal of the slope of l1.
This relationship between perpendicular lines and their slopes has practical applications in various fields. For instance, in architecture, ensuring that walls are perpendicular to each other requires their slopes to be negative reciprocals. Similarly, in engineering, designing perpendicular beams or supports involves using this principle to achieve structural stability.
Understanding the connection between perpendicular lines and their slopes is an essential part of “how to find slope with points”. It enables us to identify and analyze perpendicular lines, a common occurrence in geometry and real-world applications.
| Perpendicular Lines | |
|---|---|
| Definition | Lines that intersect at a right angle |
| Slope Relationship | Slopes are negative reciprocals of each other |
| Applications | Architecture, engineering, design |
Applications
Understanding the significance of “how to find slope with points” lies not only in its theoretical underpinnings but also in its wide-ranging applications across diverse disciplines. From geometry to economics, finding slope plays a crucial role in solving problems, making predictions, and designing solutions.
-
Facet 1: Geometry
In geometry, finding slope is essential for determining the angle of inclination of lines, calculating the area of triangles and parallelograms, and analyzing the properties of geometric shapes. It enables architects and engineers to design structures with precise angles and dimensions.
-
Facet 2: Calculus
In calculus, finding slope is central to understanding the rate of change of functions. It is used to determine the velocity and acceleration of objects in physics, the marginal cost and revenue in economics, and the instantaneous rate of change in various scientific and engineering applications.
-
Facet 3: Physics
In physics, finding slope is vital for analyzing motion, forces, and energy. It is used to determine the velocity and acceleration of objects, the angle of projectiles, and the efficiency of machines. Engineers and scientists rely on slope to design efficient engines, predict projectile trajectories, and analyze the forces acting on structures.
-
Facet 4: Economics
In economics, finding slope is crucial for understanding the relationship between supply and demand, determining the elasticity of goods, and forecasting market trends. It enables economists to analyze the impact of government policies, predict consumer behavior, and optimize resource allocation.
These diverse applications highlight the practical significance of “how to find slope with points”. By mastering this concept, individuals gain a powerful tool that can be applied to solve problems, make informed decisions, and contribute to advancements in various fields.
Example
This example is a practical illustration of the concept of slope and its significance in “how to find slope with points”. The slope of a line represents its steepness or inclination, and it is calculated as the ratio of the change in y-coordinates to the change in x-coordinates between two points on the line.
In the given example, the slope is 2, which means that for every 1 unit increase in the x-coordinate, the y-coordinate increases by 2 units. This relationship can be visualized as a straight line that rises 2 units for every 1 unit it moves to the right.
Understanding this connection is crucial because it allows us to analyze and predict the behavior of lines. In real-world applications, slope plays a vital role in various fields:
- In physics, the slope of a velocity-time graph represents the acceleration of an object.
- In economics, the slope of a demand curve indicates the responsiveness of consumers to changes in price.
- In engineering, the slope of a roof determines the angle of inclination for water drainage.
By comprehending the relationship between slope and the change in coordinates, we gain a deeper understanding of how to find slope with points and its practical significance in various disciplines.
FAQs on “How to Find Slope with Points”
This section addresses commonly asked questions and misconceptions regarding “how to find slope with points.” It provides concise and informative answers to enhance your understanding of this fundamental concept.
Question 1: What is the formula for finding the slope of a line?
The formula for finding the slope of a line is: Slope = (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) represent the coordinates of two distinct points on the line.
Question 2: What does a positive slope indicate?
A positive slope indicates that as the x-coordinate of a point on the line increases, the y-coordinate also increases. This represents an upward trend.
Question 3: What does a negative slope indicate?
A negative slope indicates that as the x-coordinate of a point on the line increases, the y-coordinate decreases. This represents a downward trend.
Question 4: What is the slope of a horizontal line?
The slope of a horizontal line is 0. This is because the y-coordinates of all points on a horizontal line are the same, resulting in no change in the y-coordinate as the x-coordinate changes.
Question 5: What is the slope of a vertical line?
The slope of a vertical line is undefined. This is because the x-coordinates of all points on a vertical line are the same, resulting in no change in the x-coordinate as the y-coordinate changes.
Question 6: How is slope used in real-world applications?
Slope finds applications in various fields, including physics (calculating velocity and acceleration), economics (analyzing supply and demand), and engineering (designing structures and systems).
Summary:
Understanding “how to find slope with points” is essential for analyzing and interpreting the behavior of lines. The slope provides valuable insights into the direction and steepness of a line, and it is calculated using the formula (y2 – y1) / (x2 – x1). By comprehending the concepts and applications of slope, individuals can effectively solve problems and make informed decisions in various disciplines.
Transition to the next article section:
In the next section, we will explore advanced techniques for finding the slope of lines, including using calculus and trigonometry.
Tips on “How to Find Slope with Points”
Understanding the concept and applications of slope is crucial in various disciplines. Here are some valuable tips to enhance your skills in finding slope with points:
Tip 1: Understand the Formula Thoroughly
The slope formula, (y2 – y1) / (x2 – x1), is the foundation for finding slope. Ensure you understand how to apply it correctly. Practice with different sets of points to gain proficiency.
Tip 2: Identify the Coordinates Accurately
Accurate identification of the coordinates (x1, y1) and (x2, y2) of the two points on the line is essential. Double-check the coordinates to avoid errors in slope calculation.
Tip 3: Consider Special Cases
Be mindful of special cases such as horizontal and vertical lines. Horizontal lines have a slope of 0, while vertical lines have an undefined slope. Understanding these special cases will help you handle them efficiently.
Tip 4: Utilize Graphing Tools
Graphing tools like graphing calculators or online graphing software can aid in visualizing the line and finding its slope. Plot the two points and use the tools to determine the slope accurately.
Tip 5: Practice Regularly
Regular practice is key to mastering the skill of finding slope with points. Solve various problems involving slope calculation to improve your speed and accuracy.
Summary:
By following these tips, you can effectively find the slope of lines using points. Remember to understand the formula, identify coordinates precisely, consider special cases, leverage graphing tools, and practice regularly to enhance your proficiency.
Transition to the article’s conclusion:
In conclusion, “how to find slope with points” is a fundamental concept with wide-ranging applications. By mastering these tips, you will gain a solid foundation in finding slope and apply it confidently in your studies or professional endeavors.
Conclusion
In conclusion, “how to find slope with points” is a foundational concept in mathematics, with profound implications in science, engineering, and economics. Through the exploration of its definition, formula, interpretation, and applications, this article has provided a comprehensive understanding of this crucial topic.
Understanding slope empowers individuals to analyze the steepness and direction of lines, solve real-world problems, and make informed decisions. By mastering the techniques of finding slope with points, one gains a valuable skill that can be applied in diverse fields, enabling advancements and discoveries.
Youtube Video:
