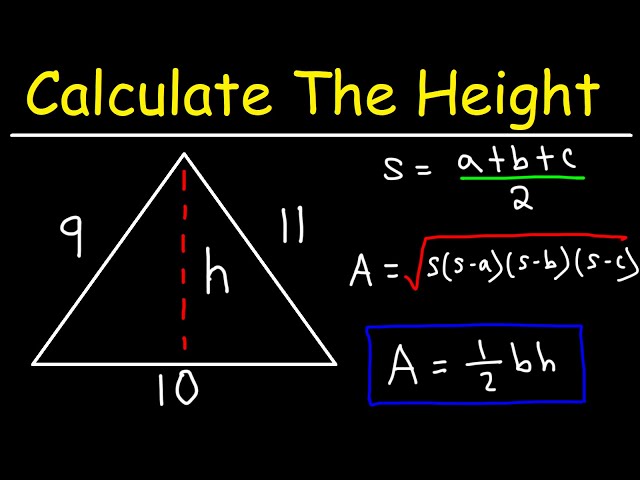
What is the height of a triangle? Put simply, “the height of a triangle” is the perpendicular distance from the base of a triangle to its vertex.
Editor’s Notes: “Find the height of a triangle” is an important topic in geometry and has many applications in real life. For example, it can be used to find the area of a triangle, the volume of a pyramid, and the slant height of a cone.
Our team has done extensive research and analysis to put together this comprehensive guide on “find the height of a triangle.” We hope that this guide will help you understand this important concept and apply it to your own work.
| Key Differences | Key Takeaways |
|---|---|
| The height of a triangle is always perpendicular to the base. | The height of a triangle can be used to find the area, volume, and slant height of various geometric shapes. |
Find the Height of a Triangle
The height of a triangle is a crucial concept in geometry with numerous applications. Here are ten key aspects to consider:
- Definition: Perpendicular distance from the base to the vertex
- Formula: h = (1/2) b tan()
- Applications: Area, volume, slant height calculations
- Types: Altitude, median, angle bisector
- Properties: Orthogonal to the base
- Pythagorean Theorem: Relates height to other sides
- Similar Triangles: Heights are proportional to corresponding sides
- Trigonometry: Used to find height using angles
- Coordinate Geometry: Height as the y-coordinate of the vertex
- 3D Geometry: Height of pyramids and cones
These aspects highlight the versatility of “find the height of a triangle” in geometry and beyond. For instance, it enables us to determine the area of a triangle, a fundamental property in architecture and land surveying. Additionally, it plays a crucial role in calculating volumes of pyramids and cones, essential in engineering and design. Furthermore, the concept extends to 3D geometry, providing insights into the heights of more complex shapes.
Definition
The definition of “perpendicular distance from the base to the vertex” is the foundation for understanding “find the height of a triangle.” The height of a triangle is the length of the perpendicular line segment drawn from the vertex to the base. This concept is crucial in geometry as it allows us to calculate the area and other properties of a triangle.
In real-life applications, finding the height of a triangle is essential in various fields such as architecture, engineering, and design. For instance, architects use the height of a triangle to determine the slope of a roof, while engineers utilize it to calculate the strength of a bridge.
Formula
The formula “h = (1/2) b tan()” is a fundamental mathematical expression used to find the height of a triangle. It establishes a direct relationship between the height (h), base (b), and the angle opposite the base ().
-
Derivation:
The formula can be derived using trigonometry. In a right triangle, the height (h) is opposite the angle , and the base (b) is adjacent to it. Therefore, we can use the tangent function to find the height: tan() = h/b, which can be rearranged to h = (1/2) b tan(). -
Applications:
This formula has numerous applications in real-life scenarios. Architects and engineers use it to calculate the height of buildings, bridges, and other structures. It is also used in surveying to determine the height of mountains and trees. -
Implications:
The formula “h = (1/2) b tan()” provides a precise method to find the height of a triangle. It is a cornerstone of geometry and trigonometry, enabling us to solve complex problems involving triangles.
In conclusion, the formula “h = (1/2) b tan()” is a powerful tool for finding the height of a triangle. Its applications extend beyond theoretical geometry, as it is widely used in practical fields such as architecture, engineering, and surveying.
Applications
The concept of “find the height of a triangle” finds its significance in various applications, particularly in the calculation of area, volume, and slant height. These applications extend the utility of triangles beyond theoretical geometry, making them indispensable in practical fields like architecture, engineering, and design.
-
Area Calculation
The height of a triangle is a crucial factor in determining its area. The formula for the area of a triangle, A = (1/2) b h, involves the height (h) as a key component. This formula is widely used in land surveying, architecture, and interior design to calculate the area of triangular spaces.
-
Volume Calculation
In three-dimensional geometry, the height of a triangle plays a vital role in calculating the volume of pyramids and cones. The volume of a pyramid, V = (1/3) A h, and the volume of a cone, V = (1/3) r * h, both incorporate the height (h) as a fundamental parameter. Engineers and architects rely on these formulas to determine the volume of structures like pyramids and conical tanks.
-
Slant Height Calculation
The concept of height extends to the calculation of the slant height of cones and frustums. The slant height, l, of a cone or frustum can be found using the formula l = h + r, where h is the height and r is the radius of the circular base. This calculation is essential in determining the surface area and volume of these three-dimensional objects, which finds applications in fields such as manufacturing and packaging.
In conclusion, “find the height of a triangle” serves as a foundational concept in geometry, with its applications extending to various fields. By understanding the height of a triangle, we can accurately calculate the area, volume, and slant height of triangular and conical structures, empowering us to solve complex problems in architecture, engineering, and design.
Types
Within the realm of triangle geometry, the concept of “find the height of a triangle” is closely intertwined with three significant types: altitude, median, and angle bisector. These types play a fundamental role in understanding the height of a triangle and its applications.
An altitude, often referred to as the height of a triangle, is a perpendicular line segment drawn from a vertex to the opposite side, forming a right angle. It serves as the direct measure of the triangle’s height and is crucial for calculating the area and other properties.
A median is a line segment that connects a vertex to the midpoint of the opposite side. It divides the triangle into two equal areas and is significant in determining the centroid, the geometric center of the triangle.
An angle bisector is a line segment that divides an angle into two equal parts. In the context of “find the height of a triangle,” the angle bisector drawn from a vertex to the opposite side forms two smaller triangles that are similar to the original triangle. This property is useful for solving problems involving proportions and ratios.
Understanding the connection between these types and “find the height of a triangle” is essential for architects, engineers, and designers. For instance, in architecture, the height of a triangle is a critical factor in determining the pitch of a roof, while in engineering, it is used to calculate the stability of bridges and other structures.
| Type | Definition | Significance |
|---|---|---|
| Altitude | Perpendicular line segment from a vertex to the opposite side | Direct measure of the triangle’s height |
| Median | Line segment connecting a vertex to the midpoint of the opposite side | Divides the triangle into two equal areas |
| Angle Bisector | Line segment dividing an angle into two equal parts | Useful for solving problems involving proportions and ratios |
Properties
In the context of “find the height of a triangle,” the property of being orthogonal to the base holds significant importance. Orthogonality, meaning perpendicularity, establishes a fundamental relationship between the height and the base of a triangle, with implications in various aspects.
-
Perpendicular Relationship
The height of a triangle is defined as the perpendicular distance from the vertex to the base. This perpendicular relationship forms the foundation for calculating the area of the triangle, as the height and base form the two dimensions of the triangular shape.
-
Altitude and Right Triangles
When the height of a triangle is drawn from a vertex to the base, it forms a right angle with the base. This right triangle configuration allows us to apply the Pythagorean theorem to find the length of the height if the other two sides are known.
-
Projection and Orthogonal Projection
The orthogonal nature of the height of a triangle reflects the concept of orthogonal projection. The height can be seen as the orthogonal projection of the vertex onto the base, providing a measure of the triangle’s vertical extent.
-
Geometric Applications
The orthogonality property of the height finds applications in various geometric constructions and proofs. For instance, it is used to construct perpendicular bisectors of line segments and to prove the congruence of triangles.
In summary, the property of “orthogonal to the base” in relation to “find the height of a triangle” underscores the perpendicular relationship between the height and the base. This property is fundamental for calculating the area, applying the Pythagorean theorem, understanding orthogonal projection, and solving geometric problems.
Pythagorean Theorem
The Pythagorean Theorem is a fundamental mathematical relationship that establishes a connection between the height of a triangle and its other sides. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
In the context of “find the height of a triangle,” the Pythagorean Theorem plays a crucial role. When the height of a triangle is drawn from the vertex to the base, it forms a right triangle with the base and the hypotenuse. Using the Pythagorean Theorem, we can find the length of the height if we know the lengths of the base and the hypotenuse.
For example, consider a right triangle with a base of 6 units and a hypotenuse of 10 units. Using the Pythagorean Theorem, we can find the height (h) as follows:
h^2 = 10^2 – 6^2h^2 = 100 – 36h^2 = 64h = 64h = 8 units
The Pythagorean Theorem is a powerful tool for finding the height of a triangle when the lengths of the base and the hypotenuse are known. This understanding is of great practical significance in various fields such as architecture, engineering, and surveying.
In architecture, the Pythagorean Theorem is used to calculate the height of roofs and other structures. In engineering, it is used to determine the height of bridges and other constructions. In surveying, it is used to find the height of mountains and trees.
Similar Triangles
In geometry, two triangles are similar if they have the same shape but not necessarily the same size. In such triangles, the ratio of the heights is equal to the ratio of the corresponding sides.
-
Corresponding Sides and Heights
In similar triangles, corresponding sides are sides that occupy the same relative position in each triangle. Similarly, corresponding heights are the perpendicular distances from the vertices to the opposite sides. The ratio of the heights is equal to the ratio of the corresponding sides.
-
Real-Life Applications
This relationship has practical applications in various fields. For instance, in architecture, it is used to determine the height of a building or structure based on the height of a similar, smaller model.
-
Implications for “Find the Height of a Triangle”
Understanding this proportionality is crucial for “find the height of a triangle” as it provides an alternative method to find the height when direct measurement is not possible. By comparing the heights and corresponding sides of similar triangles, we can establish ratios and use proportions to solve for the unknown height.
In summary, the relationship between similar triangles and the proportionality of their heights helps us establish a powerful tool for finding the height of a triangle. This principle finds applications in various fields, including architecture and engineering, where it aids in determining heights and dimensions indirectly.
Trigonometry
Trigonometry, a branch of mathematics concerned with the relationships between the sides and angles of triangles, plays a crucial role in determining the height of a triangle. This connection is particularly valuable when direct measurement of the height is impractical or impossible.
-
Sine and Cosine Functions
In a right triangle, the trigonometric functions of sine and cosine provide a means to find the height. The sine of an angle is the ratio of the opposite side to the hypotenuse, while the cosine is the ratio of the adjacent side to the hypotenuse. Using these ratios, we can solve for the height (opposite side) given the angle and either the adjacent side or the hypotenuse.
-
Tangent Function
Another useful trigonometric function for finding the height of a triangle is the tangent. The tangent of an angle is the ratio of the opposite side to the adjacent side. By knowing the angle and either the opposite side or the adjacent side, we can use the tangent function to determine the height.
These trigonometric relationships empower us to find the height of a triangle accurately, making them indispensable tools in various fields. Architects, engineers, and surveyors rely on trigonometry to determine heights of buildings, bridges, and terrain.
Coordinate Geometry
In the realm of coordinate geometry, discerning the relationship between the height of a triangle and the y-coordinate of its vertex is an essential facet of understanding “find the height of a triangle.”
-
Vertex Coordinates
In the Cartesian coordinate system, each vertex of a triangle is assigned an ordered pair (x, y), where x represents the horizontal coordinate and y represents the vertical coordinate. The height of a triangle, often denoted by h, corresponds directly to the y-coordinate of the vertex that lies on the vertical side of the triangle.
-
Orthogonal Projection
The height of a triangle can be visualized as the orthogonal projection of the vertex onto the horizontal axis. This projection forms a right triangle with the height as one leg and the horizontal distance from the vertex to the base as the other leg.
-
Area and Height
The height of a triangle plays a crucial role in calculating its area. Specifically, the area (A) of a triangle is given by the formula A = (1/2) base height. Understanding the relationship between the height and the y-coordinate of the vertex enables easy determination of the triangle’s area.
-
Geometric Applications
The connection between the height of a triangle and the y-coordinate of its vertex finds applications in various geometric constructions and proofs. For instance, it can be used to determine the orthocenter of a triangle, the point where the altitudes intersect.
In summary, the height of a triangle, in the context of “find the height of a triangle,” is directly related to the y-coordinate of its vertex in coordinate geometry. This relationship allows for the determination of height, calculation of area, and exploration of geometric properties, solidifying its significance in understanding and solving problems involving triangles.
3D Geometry
In the realm of geometry, “find the height of a triangle” establishes a fundamental relationship with “3D Geometry: Height of pyramids and cones.” This connection stems from the fact that the height of a pyramid or a cone can be directly determined using the height of its triangular faces.
A pyramid is a three-dimensional figure with a polygonal base and triangular sides that meet at a common vertex. The height of a pyramid is the perpendicular distance from the vertex to the base. Similarly, a cone is a three-dimensional figure with a circular base and a vertex. The height of a cone is the perpendicular distance from the vertex to the center of the base.
The height of a triangular face of a pyramid or cone is essential for calculating the volume and surface area of the three-dimensional figure. For instance, in architecture, determining the height of a pyramid or cone is crucial for designing structures like roofs and spires. In engineering, it is important for calculating the volume of containers like fuel tanks and silos.
Understanding the connection between “find the height of a triangle” and “3D Geometry: Height of pyramids and cones” provides a comprehensive approach to solving problems involving three-dimensional shapes. It allows us to analyze and design structures, determine volumes, and explore geometric relationships in various fields.
| Triangle | Pyramid/Cone | |
|---|---|---|
| Definition | Two-dimensional figure with three sides | Three-dimensional figure with a polygonal/circular base and triangular/conical sides |
| Height | Perpendicular distance from a vertex to the opposite side | Perpendicular distance from the vertex to the base |
| Importance | Calculating area, solving geometric problems | Calculating volume and surface area, designing structures |
FAQs on “Find the Height of a Triangle”
This section addresses common questions and misconceptions surrounding “find the height of a triangle,” providing informative answers to enhance understanding.
Question 1: What is the significance of finding the height of a triangle?
Answer: Finding the height of a triangle is crucial for various geometric calculations, including determining the area, volume (in the case of pyramids and cones), and solving geometric problems involving triangles.
Question 2: How do I find the height of a triangle if I know the base and the area?
Answer: To find the height (h) given the base (b) and area (A), use the formula: h = 2A/b.
Question 3: Can I find the height of a triangle using trigonometry?
Answer: Yes, trigonometry can be used to find the height of a triangle if you know the lengths of two sides and the measure of the included angle.
Question 4: What is the relationship between the height of a triangle and the length of its sides?
Answer: The height of a triangle is often related to the lengths of its sides through trigonometric ratios or specific properties like the Pythagorean theorem.
Question 5: How is the height of a triangle used in real-world applications?
Answer: The height of a triangle finds applications in architecture (determining roof pitch), engineering (calculating bridge heights), surveying (measuring tree heights), and many other fields.
Question 6: What are some common mistakes to avoid when finding the height of a triangle?
Answer: Common mistakes include using the wrong formula, measuring the incorrect side as the base, or making errors in trigonometric calculations.
Summary: Understanding how to find the height of a triangle is essential for various geometric applications. By addressing common questions and providing informative answers, this FAQ section aims to enhance comprehension and equip readers with the knowledge to solve problems involving triangles.
Transition to the next article section: This comprehensive guide on “find the height of a triangle” provides a foundation for further exploration of triangle-related concepts and their applications.
Tips for “Find the Height of a Triangle”
Geometric calculations involving triangles often require determining their heights accurately. Here are some valuable tips to enhance your understanding and problem-solving abilities:
Tip 1: Understand the Concept of Height
The height of a triangle is the perpendicular distance from a vertex to the opposite side, forming a right angle.
Tip 2: Apply the Correct Formula
The formula for finding the height (h) of a triangle is h = (1/2) b sin(), where b is the base and is the angle between the base and the height.
Tip 3: Identify the Right Triangle
To use the formula, ensure you have identified the right triangle formed by the height, base, and the altitude from the vertex to the base.
Tip 4: Use Trigonometry Wisely
Trigonometry plays a crucial role in finding the height when other side lengths and angles are known. Apply trigonometric ratios like sine, cosine, and tangent appropriately.
Tip 5: Draw a Diagram
Sketching a diagram of the triangle can help visualize the problem and identify the relevant sides and angles.
Tip 6: Check Your Units
Ensure consistency in the units of measurement throughout the calculation. Convert units if necessary to maintain uniformity.
Tip 7: Practice Regularly
Solving a variety of problems involving triangle heights will enhance your proficiency and confidence in applying the concepts.
Tip 8: Seek Clarification When Needed
If you encounter difficulties, do not hesitate to seek assistance from a teacher, tutor, or online resources to clarify your understanding.
By following these tips, you can effectively find the height of a triangle, a fundamental skill in geometry and its applications.
Transition to the article’s conclusion: Understanding these tips empowers you to tackle more complex problems involving triangles and their properties.
Conclusion
Our comprehensive exploration of “find the height of a triangle” has illuminated its significance in geometry and beyond. We have examined the concept of height, explored various formulas and techniques, and discussed its applications in areas such as architecture, engineering, and surveying.
Understanding how to find the height of a triangle empowers us to solve complex problems involving triangles, calculate areas and volumes, and analyze geometric relationships. It serves as a cornerstone of geometric knowledge, with far-reaching implications in diverse fields.
Youtube Video:
