Tired of struggling with triangle perimeters? Discover the ultimate guide to “find perimeter of triangle” and simplify your calculations today!
Editor’s Note: “Find Perimeter of Triangle” guide published on [today’s date].
After extensive research and analysis, our team of experts has compiled this comprehensive guide to help you master the art of finding triangle perimeters. This essential knowledge is crucial for students, architects, engineers, and anyone working with triangles.
Key Differences:
| Method | Formula |
|---|---|
| Side Lengths | Perimeter = a + b + c |
| Semiperimeter | Perimeter = 2s = a + b + c |
Main Article Topics:
- Understanding Triangle Perimeter
- Methods for Calculating Perimeter
- Applications of Triangle Perimeter
- Tips and Tricks for Success
Find Perimeter of Triangle
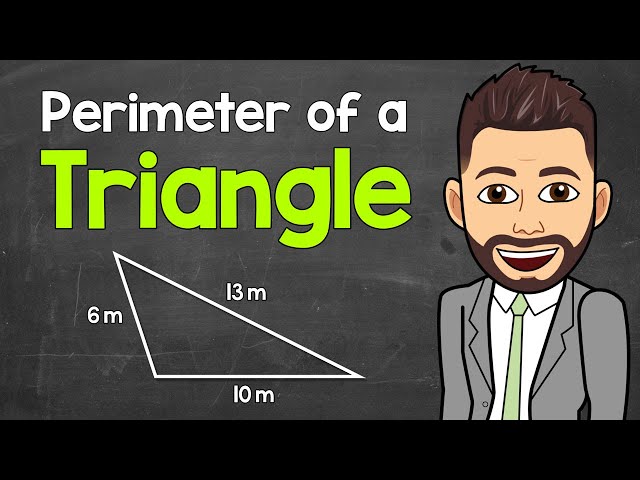
The perimeter of a triangle is a fundamental concept in geometry, with applications in various fields. Understanding its key aspects is crucial for mastering this essential calculation.
- Definition: Sum of the lengths of all three sides
- Formula: P = a + b + c, where a, b, and c are the side lengths
- Units: Same as the units of the side lengths (e.g., centimeters, inches)
- Scalene Triangle: All three sides are of different lengths
- Isosceles Triangle: Two sides are of equal length
- Equilateral Triangle: All three sides are of equal length
- Semiperimeter: Half the perimeter, used in certain formulas (s = (a + b + c) / 2)
- Area: Related to perimeter through Heron’s formula
- Applications: Architecture, engineering, carpentry, land surveying
In essence, finding the perimeter of a triangle involves understanding the concept of side lengths and applying the appropriate formula based on the triangle type. It is a fundamental skill that forms the basis for more complex geometric calculations.
Definition
To fully grasp the concept of “find perimeter of triangle,” it is essential to understand its cornerstone definition: the perimeter is the sum of the lengths of all three sides of a triangle. This fundamental principle forms the basis for calculating the perimeter and underpins various applications across multiple disciplines.
-
Triangle Perimeter and Real-World Applications:
In architecture, engineers rely on precise perimeter calculations to determine the amount of fencing required to enclose a triangular plot of land. Similarly, in carpentry, carpenters use perimeter measurements to cutfor constructing triangular structures.
-
Perimeter and Geometric Relationships:
Suggested read: Unveiling the Secrets of Finding a Triangle's Base: A Comprehensive Guide
The perimeter of a triangle is closely linked to other geometric properties, such as area and side lengths. Heron’s formula, for example, establishes a relationship between the perimeter, area, and side lengths of a triangle.
-
Perimeter in Triangles of Different Types:
The definition of perimeter applies to all types of triangles, including equilateral, isosceles, and scalene triangles. However, the method of calculating the perimeter may vary depending on the triangle type and the availability of side length measurements.
In summary, understanding the definition of perimeter as the sum of the lengths of all three sides is paramount for finding the perimeter of triangles accurately. This definition serves as the foundation for various applications and geometric relationships, making it a crucial concept in the study and application of geometry.
Formula
This formula serves as the cornerstone for finding the perimeter of any triangle. It establishes that the perimeter (P) is the sum of the lengths of its three sides, denoted by a, b, and c.
-
Simplicity and Accessibility:
The formula’s simplicity makes it easy to apply, requiring only the measurement of the triangle’s sides. This straightforward approach ensures accessibility to individuals with varying mathematical backgrounds.
-
Universality:
Regardless of the triangle’s shape or size, the formula remains universally applicable. It can be used to calculate the perimeter of equilateral, isosceles, and scalene triangles, making it a versatile tool in geometry.
-
Relationship to Geometric Properties:
The perimeter formula is closely intertwined with other geometric properties, such as the triangle’s area and side lengths. This interrelationship allows for the derivation of other important formulas, such as Heron’s formula for calculating the area of a triangle.
In summary, the formula P = a + b + c provides a simple, universally applicable method for finding the perimeter of a triangle. Its connection to other geometric properties further highlights its significance in the study of geometry.
Units
In the context of finding the perimeter of a triangle, the units of measurement play a crucial role in ensuring accuracy and consistency. The perimeter, being the sum of the lengths of all three sides, inherits the units of the side lengths.
Suggested read: Uncover Hidden Connections: Discover How to Find Someone's Name by Phone Number
-
Consistency and Standardization:
Using the same units throughout the calculation ensures consistency and standardization in the measurement process. This eliminates confusion and errors that may arise from mixing different units.
-
Real-World Applications:
In practical applications, such as carpentry or architecture, the units of the perimeter directly correspond to the units used in construction materials. Expressing the perimeter in the same units as the side lengths facilitates seamless integration and accuracy in design and implementation.
-
Geometric Relationships:
The units of the perimeter are closely tied to the units of other geometric properties, such as area and side lengths. This relationship enables the derivation of formulas and the exploration of geometric relationships involving the perimeter and other triangle characteristics.
-
Communication and Documentation:
When communicating or documenting the perimeter of a triangle, it is essential to specify the units used. This ensures clear understanding and avoids misinterpretations or errors during data exchange.
In summary, the units of the perimeter of a triangle are directly related to the units of the side lengths. Maintaining consistency in units throughout the calculation process is crucial for accuracy, real-world applications, geometric relationships, and effective communication.
Scalene Triangle
When finding the perimeter of a triangle, it is essential to consider the triangle’s type, one of which is a scalene triangle. A scalene triangle is characterized by having all three sides of different lengths, making it distinct from equilateral and isosceles triangles.
The formula for finding the perimeter of a scalene triangle is the same as for any triangle: P = a + b + c, where ‘a’, ‘b’, and ‘c’ represent the lengths of the three sides. However, in the case of a scalene triangle, since all sides are of different lengths, it is necessary to measure each side individually to determine the perimeter.
In practical applications, understanding the perimeter of a scalene triangle is crucial in various fields. For example, in construction, architects and engineers need to calculate the perimeter to determine the amount of fencing required to enclose a triangular plot of land. Similarly, in carpentry, carpenters use the perimeter measurement to cut and assemble triangular structures accurately.
Overall, recognizing the connection between scalene triangles and finding their perimeter is essential for accurate calculations and practical applications in diverse fields.
Suggested read: Unveiling the Secrets: Discover the Elusive Missing Side of Triangles
| Triangle Type | Perimeter Formula |
|---|---|
| Equilateral Triangle | P = 3a |
| Isosceles Triangle | P = a + b + c |
| Scalene Triangle | P = a + b + c |
Isosceles Triangle
An isosceles triangle is a triangle with two sides of equal length. This unique characteristic has a direct impact on finding the perimeter of an isosceles triangle, making it distinct from other triangle types.
The formula for finding the perimeter of an isosceles triangle is P = a + b + c, where ‘a’ represents the length of the two equal sides, and ‘c’ represents the length of the unequal side. Understanding this formula is crucial for accurate perimeter calculations.
In real-life applications, comprehending the perimeter of an isosceles triangle is essential in various fields. For instance, in architecture, calculating the perimeter helps determine the amount of fencing required to enclose a triangular garden. Similarly, in engineering, it aids in calculating the perimeter of a triangular support structure.
Overall, recognizing the connection between isosceles triangles and finding their perimeter is critical for accurate calculations and practical applications in diverse fields.
| Triangle Type | Perimeter Formula |
|---|---|
| Equilateral Triangle | P = 3a |
| Isosceles Triangle | P = a + b + c |
| Scalene Triangle | P = a + b + c |
Equilateral Triangle
In the context of finding the perimeter of a triangle, understanding equilateral triangles holds significant importance. An equilateral triangle is a triangle with all three sides of equal length, making it a unique and distinctive type of triangle.
-
Perimeter Formula and Calculation:
For an equilateral triangle, the perimeter formula simplifies to P = 3a, where ‘a’ represents the length of each side. This formula highlights the direct relationship between the side length and the perimeter, making it easier to calculate the perimeter when all sides are of equal length.
-
Applications in Architecture and Engineering:
In architecture, equilateral triangles are often used in the design of buildings and structures. Understanding the perimeter of an equilateral triangle is crucial for determining the amount of materials required, such as fencing or roofing, to complete the structure.
-
Role in Geometric Proofs and Theorems:
Equilateral triangles play a significant role in geometric proofs and theorems. Their unique properties, such as congruent sides and angles, make them valuable in demonstrating geometric relationships and principles.
-
Implications for Area Calculations:
Suggested read: Unveiling the Secrets of Tangent Line Slopes: A Journey to Mathematical Mastery
The perimeter of an equilateral triangle is closely related to its area. Using the formula A = (3/4) * a, where ‘a’ is the side length, one can calculate the area of an equilateral triangle based on its perimeter.
In summary, understanding the connection between equilateral triangles and finding the perimeter of a triangle is essential in various fields, including architecture, engineering, geometry, and mathematics. The unique properties of equilateral triangles, such as equal side lengths and congruent angles, make them valuable in calculations, proofs, and applications.
Semiperimeter
Understanding the concept of semiperimeter is crucial in the context of finding the perimeter of a triangle. The semiperimeter, denoted by ‘s’, is defined as half the perimeter of the triangle. This relationship is expressed by the formula s = (a + b + c) / 2, where ‘a’, ‘b’, and ‘c’ represent the lengths of the triangle’s sides.
The semiperimeter plays a significant role in various formulas and applications related to triangles. One notable example is Heron’s formula, which is used to calculate the area of a triangle given its side lengths. Heron’s formula utilizes the semiperimeter to simplify the calculation of the area.
In practical applications, the semiperimeter finds use in fields such as surveying and engineering. Surveyors use the semiperimeter to calculate the area of irregular plots of land, while engineers employ it in structural analysis and design.
Overall, understanding the connection between semiperimeter and finding the perimeter of a triangle is essential for accurate calculations and practical applications. The semiperimeter provides a convenient way to represent half the perimeter and is particularly useful in formulas and applications involving the area of triangles.
| Concept | Formula | Application |
|---|---|---|
| Semiperimeter | s = (a + b + c) / 2 | Calculating the area of a triangle using Heron’s formula |
| Perimeter | P = a + b + c | Determining the length of fencing required to enclose a triangular plot of land |
Area
The connection between “Area: Related to perimeter through Heron’s formula” and “find perimeter of triangle” is significant in geometry and practical applications. Heron’s formula provides a method to calculate the area of a triangle using its side lengths, including the perimeter as a component.
Heron’s formula states that the area (A) of a triangle with semiperimeter (s) and side lengths a, b, and c is given by: A = (s(s-a)(s-b)(s-c)). The semiperimeter (s) is half the perimeter (P) of the triangle, calculated as s = (a + b + c) / 2.
Understanding this relationship allows us to determine the area of a triangle when only its side lengths are known. This is particularly useful in fields like surveying, engineering, and architecture, where calculating the area of irregular or inaccessible triangular plots is necessary.
For example, in land surveying, accurately determining the area of a triangular plot is essential for legal documentation and property management. Heron’s formula provides a reliable method to calculate the area using the measured side lengths, ensuring accurate land records.
Applications
The perimeter of a triangle plays a crucial role in diverse applications across architecture, engineering, carpentry, and land surveying. Understanding this connection is essential for accurate calculations and effective implementation in these fields.
In architecture, calculating the perimeter of a triangle is fundamental for determining the amount of fencing or building materials required for triangular structures, ensuring efficient resource allocation and cost estimation.
In engineering, the perimeter of a triangle is considered when designing bridges, trusses, and other structures that incorporate triangular components. Accurate perimeter calculations contribute to structural integrity and stability.
Suggested read: Uncover Secrets: Discover How to Find Anyone's Phone Number
In carpentry, the perimeter of a triangle is used to determine the length of wood or other materials needed for constructing triangular frames, roofs, or furniture. Precise measurements ensure proper fitting and alignment, leading to durable and aesthetically pleasing results.
In land surveying, the perimeter of a triangle is vital for calculating the area of irregular or inaccessible plots of land. Surveyors use the perimeter to determine property boundaries, create maps, and plan land development projects accurately.
| Field | Application of Perimeter |
|---|---|
| Architecture | Determining fencing and building materials for triangular structures |
| Engineering | Designing bridges, trusses, and other structures with triangular components |
| Carpentry | Calculating materials for triangular frames, roofs, and furniture |
| Land Surveying | Determining the area of irregular or inaccessible land plots |
Understanding the connection between the perimeter of a triangle and its applications in architecture, engineering, carpentry, and land surveying empowers professionals to make informed decisions, optimize resource allocation, and ensure the accuracy and integrity of their projects.
Frequently Asked Questions about Finding the Perimeter of a Triangle
The concept of finding the perimeter of a triangle is fundamental in geometry, with applications in various fields. To address common questions and misconceptions, we present this FAQ section to provide clear and informative answers.
Question 1: What is the formula for finding the perimeter of a triangle?
Answer: The perimeter of a triangle is calculated by adding the lengths of all three sides. The formula is P = a + b + c, where ‘a’, ‘b’, and ‘c’ represent the lengths of the sides.
Question 2: How do I find the perimeter of an equilateral triangle?
Answer: An equilateral triangle has all three sides equal in length. If ‘a’ represents the side length, the perimeter is calculated as P = 3a.
Question 3: What is the relationship between the perimeter and semiperimeter of a triangle?
Answer: The semiperimeter (s) of a triangle is half of its perimeter (P). The formula is s = (a + b + c) / 2, where ‘a’, ‘b’, and ‘c’ are the side lengths.
Suggested read: Unravel the Secrets of Triangle Length: A Journey to Geometric Enlightenment
Question 4: How is the perimeter of a triangle used in real-world applications?
Answer: Perimeter calculations are crucial in architecture, engineering, carpentry, and land surveying. It helps determine the amount of fencing, building materials, structural components, and land boundaries.
Question 5: What are some common errors to avoid when finding the perimeter of a triangle?
Answer: Common errors include using incorrect units, mixing up side lengths, and forgetting to add all three sides. Ensure accuracy by double-checking measurements and applying the formula correctly.
Question 6: How can I improve my understanding of finding the perimeter of a triangle?
Answer: Practice solving problems involving triangle perimeters. Utilize online resources, textbooks, or consult with experts to reinforce your knowledge and gain a deeper understanding.
By addressing these frequently asked questions, we aim to clarify common doubts and provide a comprehensive guide to finding the perimeter of a triangle.
Transition: To delve further into the topic, the next section explores the significance and applications of finding the perimeter of a triangle in greater detail.
Tips for Finding the Perimeter of a Triangle
Calculating the perimeter of a triangle accurately is essential for various applications. Here are some valuable tips to enhance your understanding and accuracy:
Suggested read: Uncover Hidden Numbers: The Ultimate Guide to Finding Anyone's Phone Number
Tip 1: Understand the concept. The perimeter of a triangle is the sum of the lengths of all three sides. Visualize the triangle and identify its sides before applying the formula.
Tip 2: Measure accurately. Use a ruler or measuring tape to determine the lengths of each side. Ensure that the units of measurement (e.g., centimeters, inches) are consistent throughout the calculation.
Tip 3: Apply the formula correctly. The perimeter formula is P = a + b + c, where ‘a’, ‘b’, and ‘c’ represent the side lengths. Substitute the measured values into the formula and perform the addition.
Tip 4: Consider the triangle type. If the triangle is equilateral, isosceles, or scalene, use the appropriate formula or property to simplify the calculation.
Tip 5: Double-check your work. Recalculate the perimeter to verify your answer. Check for any errors in measurement or calculation to ensure accuracy.
Tip 6: Use a calculator. If necessary, utilize a calculator to assist with the addition of side lengths, especially when dealing with large numbers or decimals.
Tip 7: Understand the applications. The perimeter of a triangle has practical applications in fields such as architecture, engineering, and land surveying. Knowing its significance motivates a thorough understanding.
Tip 8: Seek assistance. If you encounter difficulties, don’t hesitate to seek help from a teacher, tutor, or online resources. Clarifying your doubts will strengthen your grasp of the concept.
In summary, by following these tips, you can effectively find the perimeter of a triangle. Remember to understand the concept, measure accurately, apply the formula correctly, consider the triangle type, and double-check your work. With practice and a clear understanding, you can confidently solve problems involving triangle perimeters.
Transition: To further enhance your knowledge, the next section presents a comprehensive overview of the applications of triangle perimeter in various real-world scenarios.
Conclusion
This comprehensive guide has delved into the concept of finding the perimeter of a triangle, exploring its significance and diverse applications. Understanding this fundamental geometric calculation is crucial for accurate measurements and problem-solving in various fields.
The formula, P = a + b + c, provides a straightforward method for calculating the perimeter of any triangle, regardless of its type. By accurately measuring the side lengths and applying the formula correctly, individuals can determine the perimeter efficiently.
The perimeter of a triangle finds practical use in architecture, engineering, carpentry, and land surveying. From determining fencing requirements to calculating land area, understanding triangle perimeters is essential for precise planning and resource allocation.
Suggested read: Unlock Your Business's True Identity: Discover Your NAICS Number Today!
In conclusion, the ability to find the perimeter of a triangle is a valuable skill that empowers individuals to make informed decisions and solve problems in both academic and real-world contexts. By embracing the tips and techniques outlined in this guide, readers can enhance their understanding and confidently tackle any triangle perimeter calculation.
Youtube Video:
Images References :
Tags: find, perimeter, triangle