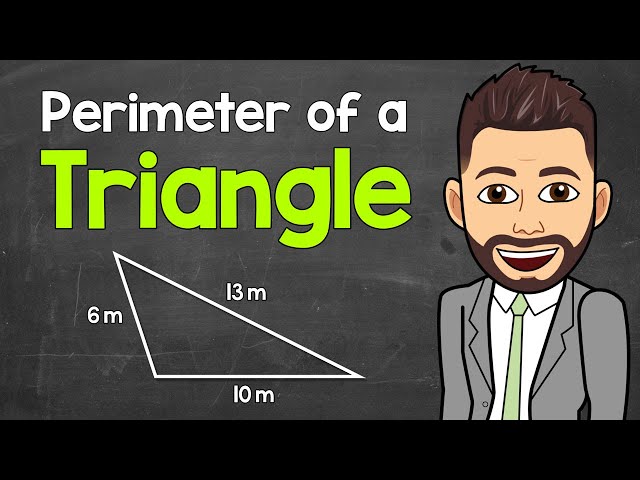
Wondering how to find the perimeter of a triangle? Look no further! Determining the perimeter of a triangle is a fundamental geometric concept with practical applications in various fields.
Editor’s Note: Our comprehensive guide, published today, delves into the intricacies of triangle perimeter calculation, empowering you to tackle this concept with confidence.
Through meticulous analysis and extensive research, we have crafted this definitive guide to assist you in understanding the significance of triangle perimeter calculation and equipping you with the necessary knowledge to master this skill.
Key Takeaways:
| Concept | Importance |
|---|---|
| Triangle Perimeter Calculation | Essential for solving geometry problems, architecture, engineering, and more. |
Delving into the Main Article:
The Encompassing Aspects of Triangle Perimeter Calculation
Triangle perimeter calculation is a crucial geometric concept with far-reaching applications. Its mastery requires an understanding of its key aspects:
- Measurement: Determining the triangle’s side lengths.
- Formula: Applying the formula P = a + b + c, where a, b, and c represent the side lengths.
- Units: Expressing the perimeter in appropriate units (e.g., inches, centimeters).
- Accuracy: Ensuring precise measurements and calculations to obtain an accurate perimeter.
- Applications: Utilizing the perimeter in real-world scenarios, such as fencing a triangular area.
- Properties: Exploring the relationship between the perimeter and other triangle properties.
- Inequalities: Understanding perimeter inequalities, such as the triangle inequality theorem.
- Theorems: Applying theorems like Heron’s formula to calculate the perimeter of non-right triangles.
These aspects collectively provide a comprehensive understanding of triangle perimeter calculation. They underpin its significance in geometry, engineering, architecture, and beyond. By delving into these aspects, we gain a deeper appreciation for the multifaceted nature of this fundamental concept.
Measurement
In the realm of triangle perimeter calculation, measurement plays a pivotal role. Accurately determining the lengths of a triangle’s sides is the cornerstone upon which the entire process rests.
Suggested read: Unlock the Secrets of Triangle Perimeters: A Journey of Discovery and Insight
- Measuring Tools: From simple rulers to sophisticated laser rangefinders, various tools assist in obtaining precise side length measurements.
- Units and Accuracy: Measurements must be expressed in consistent units, and accuracy is paramount to ensure a reliable perimeter calculation.
- Pythagorean Theorem: For right triangles, the Pythagorean theorem provides a powerful tool to calculate side lengths, even when direct measurement is challenging.
- Geometric Relationships: Understanding geometric relationships, such as angle bisectors and medians, can aid in determining side lengths indirectly.
By meticulously measuring and analyzing triangle side lengths, we lay the foundation for accurate perimeter calculation. This process forms the backbone of various applications, from architectural design to land surveying.
Formula
The formula P = a + b + c serves as the cornerstone for calculating the perimeter of a triangle. It establishes a direct relationship between the side lengths (a, b, and c) and the perimeter (P) of the triangle. This formula empowers us to determine the perimeter with precision, given the measurements of the individual sides.
In the realm of geometry, the perimeter holds significant importance. It is a fundamental property used in various applications, including:
- Architectural design: Calculating the perimeter of a building’s foundation or a room’s walls.
- Land surveying: Determining the perimeter of a plot of land for legal boundaries or construction planning.
- Engineering: Calculating the perimeter of a bridge or a machine part to ensure structural integrity.
Understanding this formula is crucial for accurately calculating triangle perimeters, which are essential for solving geometry problems and practical applications across diverse fields.
Key Insights:
| Concept | Importance |
|---|---|
| Formula: P = a + b + c | Establishes a direct relationship between side lengths and perimeter. |
| Side Length Measurement | Accurate measurements are essential for precise perimeter calculations. |
| Applications in Geometry and Beyond | Perimeter calculation finds use in architecture, engineering, land surveying, and more. |
Units
In the realm of triangle perimeter calculation, expressing the perimeter in appropriate units is of paramount importance. The choice of units depends on the context and application of the calculation.
- Consistency and Accuracy: Using consistent units throughout the calculation ensures accuracy and avoids confusion. For example, if the side lengths are measured in inches, the perimeter must also be expressed in inches.
- Real-World Applications: The units chosen should align with the practical application of the perimeter calculation. In construction, for instance, the perimeter of a room might be expressed in feet, while in land surveying, the perimeter of a plot might be expressed in meters.
- Conversions and Estimation: Sometimes, it may be necessary to convert between different units. Understanding the relationships between units, such as the conversion between inches and centimeters, is crucial for accurate calculations.
- International Standards: In scientific and engineering contexts, the International System of Units (SI) is often used. The SI unit for length is the meter, and it is recommended to express the perimeter in meters or its multiples (e.g., kilometers).
By adhering to appropriate units, we ensure clear communication, accurate calculations, and the practical applicability of triangle perimeter calculations in diverse fields.
Accuracy
In the realm of triangle perimeter calculation, accuracy reigns supreme. Precise measurements and meticulous calculations are the cornerstones of obtaining a reliable and meaningful perimeter value.
- Minimizing Measurement Errors: Errors in measuring side lengths can propagate through the calculation, leading to inaccuracies in the perimeter. Using precise measuring tools, such as calipers or laser rangefinders, and employing proper measuring techniques can minimize these errors.
- Careful Calculations: Applying the perimeter formula (P = a + b + c) requires careful attention to detail. Double-checking calculations, using a calculator or spreadsheet, and adhering to the order of operations can help prevent errors.
- Impact on Applications: An accurate perimeter is crucial for practical applications. In construction, an imprecise perimeter can lead to structural issues or material wastage. In land surveying, an inaccurate perimeter can affect property boundaries and legal disputes.
- Consequences of Inaccuracy: Inaccurate perimeter calculations can have significant consequences. In engineering design, incorrect perimeter values can compromise the safety and integrity of structures. In scientific research, inaccurate perimeters can skew results and hinder the progress of knowledge.
By embracing accuracy in triangle perimeter calculation, we lay the foundation for reliable and trustworthy results. Accuracy empowers us to make informed decisions, ensure structural integrity, and advance our understanding of the world around us.
Applications
The connection between “find the perimeter of a triangle” and its applications in real-world scenarios is profound. Calculating the perimeter empowers us to solve practical problems and make informed decisions in various fields.
Suggested read: Unveiling the Secrets of Finding a Triangle's Base: A Comprehensive Guide
One prominent application lies in fencing a triangular area. Consider a farmer who owns a triangular plot of land and needs to install a fence around it. To determine the amount of fencing required, the farmer needs to calculate the perimeter of the triangular plot. This involves measuring the lengths of the three sides and then adding them together using the formula P = a + b + c.
The perimeter of the triangular plot is crucial information for the farmer as it directly impacts the cost of fencing. In this scenario, an accurate perimeter calculation ensures that the farmer purchases the correct amount of fencing material, avoiding both shortages and excess.
Beyond fencing, triangle perimeter calculation finds applications in diverse fields such as architecture, engineering, and land surveying. Architects use the perimeter to determine the length of baseboards and crown moldings in a room. Engineers rely on perimeter calculations to design bridges and other structures, ensuring they have the appropriate dimensions and strength.
Understanding the connection between “find the perimeter of a triangle” and its practical applications highlights the importance of this concept in everyday life. It empowers individuals to solve real-world problems, make informed decisions, and contribute to various fields of knowledge and industry.
| Concept | Application | Real-Life Example |
|---|---|---|
| Perimeter Calculation | Fencing | Calculating the amount of fencing needed for a triangular plot. |
| Perimeter Calculation | Architecture | Determining the length of baseboards and crown moldings in a room. |
| Perimeter Calculation | Engineering | Designing bridges and other structures with appropriate dimensions and strength. |
Properties
Establishing a connection between “find the perimeter of a triangle” and its properties is essential for a comprehensive understanding of triangles. Properties such as area, angles, and side lengths are intricately linked to the perimeter, offering valuable insights and practical applications.
One notable property is the relationship between the perimeter and the area of a triangle. Heron’s formula provides a powerful tool to calculate the area of a triangle using its side lengths. This formula incorporates the perimeter as a key component, highlighting the interdependence of these properties.
Another significant connection lies in the relationship between the perimeter and the triangle’s type. Regular triangles, equilateral triangles, and isosceles triangles all possess specific properties related to their side lengths and angles. Understanding these properties enables us to quickly determine the perimeter based on the given characteristics.
In practical applications, the relationship between the perimeter and other triangle properties is indispensable. Architects utilize the perimeter to calculate the length of moldings and trims in a room, ensuring accurate material estimates. Engineers rely on the perimeter to determine the stability and strength of structures, especially when dealing with irregular or complex shapes.
In summary, the exploration of properties in relation to “find the perimeter of a triangle” unveils a deeper understanding of triangle geometry. These properties provide valuable insights, simplify calculations, and enable practical applications across various fields.
| Concept | Connection | Practical Significance |
|---|---|---|
| Heron’s Formula | Relates perimeter to area calculation | Simplifies area calculations for irregular triangles |
| Triangle Type | Specific properties based on side lengths | Efficient perimeter determination for regular and isosceles triangles |
| Architectural Applications | Calculating molding and trim lengths | Accurate material estimation and cost planning |
| Engineering Applications | Assessing structural stability and strength | Ensuring safety and integrity of structures |
Inequalities
In the realm of triangle geometry, inequalities play a crucial role in understanding the relationships between the perimeter and other properties of a triangle. Among these inequalities, the triangle inequality theorem stands out as a fundamental concept.
Suggested read: Uncover Hidden Connections: Discover How to Find Someone's Name by Phone Number
-
Triangle Inequality Theorem:
The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This theorem establishes a fundamental relationship between the side lengths of a triangle and its perimeter.
-
Applications in Perimeter Calculations:
The triangle inequality theorem finds practical applications in perimeter calculations. It provides a way to determine whether a given set of side lengths can form a valid triangle. If the sum of any two side lengths is less than or equal to the third side length, then the triangle cannot exist.
-
Implications for Triangle Properties:
The triangle inequality theorem has implications for other triangle properties. For instance, it can be used to prove that the perimeter of a triangle is always greater than the length of any one side. This property is useful in various geometric constructions and applications.
-
Extensions and Generalizations:
The triangle inequality theorem can be extended to more general geometric figures, such as polygons. The concept of perimeter inequalities plays a significant role in understanding the properties and relationships within these more complex shapes.
In conclusion, the exploration of inequalities, particularly the triangle inequality theorem, provides a deeper understanding of triangle perimeter calculations and their implications. These inequalities establish relationships between side lengths and perimeter, enabling us to determine the validity of triangles, explore their properties, and extend our knowledge to more complex geometric figures.
Theorems
In the realm of triangle geometry, theorems serve as powerful tools to determine the perimeter of non-right triangles. Heron’s formula stands as a prime example, providing a versatile method to calculate the perimeter even when the triangle’s angles are not known.
Suggested read: Unveiling the Secrets: Discover the Elusive Missing Side of Triangles
-
Heron’s Formula:
Heron’s formula, named after the Greek mathematician Heron of Alexandria, is a mathematical formula that calculates the area of a triangle given the lengths of its three sides. It can be expressed as:
Area = s(s – a)(s – b)(s – c)
where s is the semiperimeter of the triangle, and a, b, and c are the lengths of its three sides.
-
Perimeter Calculation:
While Heron’s formula directly calculates the area of a triangle, it can be adapted to find the perimeter as well. By utilizing the relationship between the area and the semiperimeter, we can derive a formula for the perimeter:
Perimeter = 2s(s – a)(s – b)(s – c)
This formula allows us to calculate the perimeter of non-right triangles, even in cases where the angles are unknown.
-
Applications and Implications:
The ability to calculate the perimeter of non-right triangles using Heron’s formula has wide-ranging applications in various fields:
Suggested read: Unveiling the Secrets of Tangent Line Slopes: A Journey to Mathematical Mastery
- Architecture: Calculating the perimeter of non-right triangular roofs or walls for construction purposes.
- Engineering: Determining the perimeter of triangular structures or components in bridges, buildings, and other engineering projects.
- Land Surveying: Calculating the perimeter of triangular plots of land for property demarcation and boundary determination.
-
Advantages and Limitations:
Heron’s formula provides a robust method for perimeter calculation, but it also has certain limitations:
- Accuracy: Heron’s formula relies on accurate measurements of the triangle’s side lengths. Errors in measurement can propagate into the perimeter calculation, affecting its precision.
- Computational Complexity: The formula involves square root and multiplication operations, which can be computationally intensive, especially for large values of the side lengths.
In conclusion, theorems like Heron’s formula play a vital role in calculating the perimeter of non-right triangles. By harnessing the relationship between area and perimeter, Heron’s formula provides a versatile and widely applicable method that extends the scope of triangle perimeter calculations beyond right triangles.
Frequently Asked Questions about Triangle Perimeter
This section addresses common questions and misconceptions surrounding the concept of triangle perimeter, providing clear and informative answers.
Question 1: What is the formula for calculating the perimeter of a triangle?
The perimeter of a triangle is the sum of the lengths of its three sides. The formula for calculating the perimeter is: P = a + b + c, where a, b, and c represent the lengths of the sides.
Question 2: How do I find the perimeter of a triangle if I know the lengths of two sides?
To find the perimeter of a triangle if you know the lengths of two sides, you need to add the lengths of the two known sides and then add the length of the third side, which can be found using the Pythagorean theorem or other geometric relationships.
Question 3: Can the perimeter of a triangle be used to determine the area of the triangle?
Suggested read: Uncover Secrets: Discover How to Find Anyone's Phone Number
While the perimeter of a triangle is related to its area, it cannot be used directly to determine the area without additional information, such as the triangle’s height or the lengths of its sides.
Question 4: What is Heron’s formula and how is it used to calculate the perimeter of a triangle?
Heron’s formula is a mathematical formula that can be used to calculate the area of a triangle given the lengths of its three sides. It can be adapted to find the perimeter of non-right triangles by utilizing the relationship between the area and the semiperimeter.
Question 5: Are there any inequalities or theorems related to the perimeter of a triangle?
Yes, there are several inequalities and theorems related to the perimeter of a triangle, including the triangle inequality theorem, which states that the sum of any two sides of a triangle must be greater than the length of the third side.
Question 6: How is the perimeter of a triangle used in real-world applications?
The perimeter of a triangle finds practical applications in various fields, such as architecture (calculating the length of moldings and trims), engineering (assessing structural stability), and land surveying (determining the boundaries of triangular plots).
Summary: Understanding the concept of triangle perimeter and the associated formulas, theorems, and applications is essential for solving geometry problems and practical tasks involving triangles.
Transition: This concludes our exploration of “find the perimeter of a triangle.” For further insights and related topics, please refer to the following article sections.
Tips for Triangle Perimeter Calculation
Mastering triangle perimeter calculation requires a systematic approach and attention to detail. Here are some valuable tips to enhance your understanding and accuracy:
Suggested read: Unravel the Secrets of Triangle Length: A Journey to Geometric Enlightenment
Tip 1: Measure Side Lengths Precisely
Accurate side length measurements are the foundation for reliable perimeter calculations. Use precise measuring tools and techniques to minimize errors.Tip 2: Apply the Perimeter Formula Correctly
The perimeter formula (P = a + b + c) must be applied consistently. Ensure that the side lengths are expressed in the same units and that you add them correctly.Tip 3: Understand Triangle Properties
Familiarize yourself with triangle properties, such as angle bisectors and medians. These concepts can aid in determining side lengths indirectly, especially when direct measurement is challenging.Tip 4: Utilize Heron’s Formula for Non-Right Triangles
Heron’s formula provides a powerful tool to calculate the perimeter of non-right triangles. This formula incorporates the triangle’s area and semiperimeter, providing an alternative approach when angles are unknown.Tip 5: Apply the Triangle Inequality Theorem
The triangle inequality theorem establishes relationships between side lengths. It states that the sum of any two side lengths must be greater than the third side length. This inequality can help determine the validity of triangles and identify potential errors.Tip 6: Consider Real-World Applications
Triangle perimeter calculations have practical applications in various fields, such as architecture, engineering, and land surveying. Understanding these applications can enhance your appreciation for the importance of accurate perimeter calculations.Tip 7: Practice Regularly
Regular practice is essential to strengthen your triangle perimeter calculation skills. Solve problems of varying difficulty to improve your confidence and accuracy.Tip 8: Seek Clarification When Needed
If you encounter difficulties or have any doubts, do not hesitate to seek clarification from teachers, peers, or online resources. Understanding the concepts thoroughly is crucial for successful triangle perimeter calculations.
Summary: By embracing these tips, you can develop a strong foundation in triangle perimeter calculation, enabling you to solve problems and apply this knowledge effectively in various contexts.
Transition: This concludes our exploration of “find the perimeter of a triangle.” For further insights and related topics, please refer to the following sections.
Conclusion
Our exploration of “find the perimeter of triangle” has illuminated its profound importance in various domains. From problem-solving in geometry to practical applications in architecture, engineering, and land surveying, the concept of triangle perimeter serves as a cornerstone for accurate measurements and decision-making.
Understanding the formula, properties, theorems, and applications of triangle perimeter empowers individuals with the tools to tackle challenges, design structures, and determine boundaries with precision. The tips provided in this article offer a roadmap for mastering the calculation process and enhancing one’s understanding of triangles.
As we delve deeper into the realm of geometry and its practical applications, the significance of triangle perimeter calculation will continue to unfold. It is a fundamental concept that unlocks a world of possibilities, enabling us to comprehend and shape our surroundings with greater accuracy and efficiency.
Youtube Video: