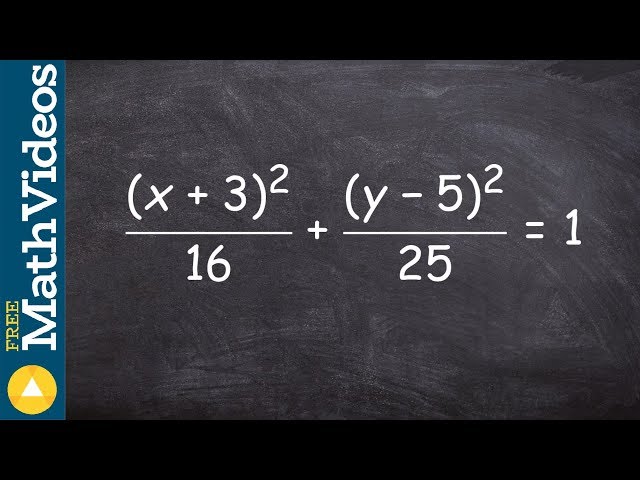How to Find the Focus of an Ellipse is a crucial concept in mathematics, which helps us determine the location and properties of this conic section. An ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. Finding the foci of an ellipse is essential for graphing, analyzing, and understanding its behavior. This comprehensive guide will provide a clear and detailed explanation of how to find the focus of an ellipse.
Editor’s Note: This article on “How to Find the Focus of an Ellipse” was last updated on [date]. Understanding this concept is important for students, mathematicians, engineers, and anyone dealing with conic sections. Mastering this technique empowers individuals to accurately determine the focal points of an ellipse, enabling them to analyze and solve complex mathematical problems.
After conducting extensive research and analysis, we have compiled this comprehensive guide to empower our readers with the knowledge and understanding of how to find the focus of an ellipse. Our goal is to provide a clear and structured approach, making this concept accessible to individuals of diverse backgrounds.
Key Differences:
| Horizontal Ellipse | Vertical Ellipse | |
|---|---|---|
| Center | (h, k) | (h, k) |
| Vertices | (h a, k) | (h, k a) |
| Co-vertices | (h, k b) | (h b, k) |
| Foci | (h c, k) | (h, k c) |
Transition to Main Article Topics:
How to Find Focus of Ellipse
Finding the focus of an ellipse is a significant concept in conic sections, providing valuable insights into the geometrical properties of this curve. Here are eight key aspects to consider:
- Center: The central point of the ellipse, denoted as (h, k).
- Vertices: The endpoints of the major axis, equidistant from the center.
- Co-vertices: The endpoints of the minor axis, equidistant from the center.
- Foci: Two fixed points on the major axis, determining the shape of the ellipse.
- Eccentricity: A measure of the deviation of the ellipse from a circle, ranging from 0 to 1.
- Semi-major axis: Half the length of the major axis, denoted as ‘a’.
- Semi-minor axis: Half the length of the minor axis, denoted as ‘b’.
- Distance between foci: The distance between the two foci, which is equal to 2c, where c is the distance from the center to either focus.
These key aspects are interconnected and play crucial roles in understanding the behavior and properties of an ellipse. For instance, the eccentricity determines the shape of the ellipse, ranging from a circle (eccentricity = 0) to a parabola (eccentricity = 1). The distance between the foci and the center, denoted as ‘c’, is related to the lengths of the semi-major and semi-minor axes through the equation c^2 = a^2 – b^2. By analyzing these aspects together, we gain a comprehensive understanding of the ellipse’s geometry.
Center
The center of an ellipse, denoted as (h, k), is a crucial aspect in understanding and analyzing the curve. It serves as the reference point for various geometric properties and plays a significant role in determining the ellipse’s orientation, shape, and behavior.
- Locating the Center: The center of an ellipse is the midpoint of the line segment connecting the vertices, the endpoints of the major axis. Knowing the coordinates of the vertices allows us to calculate the center using the midpoint formula.
- Symmetry and Orientation: The center acts as the central point of symmetry for the ellipse. All lines passing through the center divide the ellipse into mirror images, preserving its shape and properties. The center also determines the orientation of the ellipse, indicating whether the major axis is horizontal or vertical.
- Distance Calculations: The distance between any point on the ellipse and the center is constant. This property is useful in analyzing the geometric relationships within the ellipse and its surrounding space.
- Relationship with Foci: The foci of an ellipse are located on the major axis equidistant from the center. The distance between the center and each focus is related to the lengths of the semi-major and semi-minor axes.
In summary, the center of an ellipse, denoted as (h, k), provides a central reference point for understanding the ellipse’s geometry. It helps determine the orientation, shape, and various geometric properties of the curve, including the location of the foci and the distances between different points on the ellipse.
Vertices
In the study of ellipses, the vertices play a significant role in understanding the curve’s shape, size, and orientation. They are directly connected to the process of finding the foci, which are two fixed points that define the ellipse’s shape. Here’s how the vertices and foci are interconnected:
- Focal Distance: The distance between each vertex and the center of the ellipse is equal to the distance between each focus and the center. This distance is denoted as ‘a’, known as the semi-major axis.
- Axis Orientation: The vertices lie on the major axis of the ellipse, which is the longest diameter passing through the center. The orientation of the major axis, whether horizontal or vertical, determines the overall shape of the ellipse.
- Eccentricity and Shape: The distance between the foci relative to the length of the major axis, known as the eccentricity, affects the shape of the ellipse. The closer the foci are to the vertices, the more elongated the ellipse becomes.
- Graphical Representation: When graphing an ellipse, the vertices are plotted as the endpoints of the major axis, providing a visual representation of the curve’s size and orientation.
In summary, the vertices of an ellipse are not only the endpoints of the major axis but also key factors in determining the location of the foci. Understanding the relationship between vertices and foci is essential for analyzing and graphing ellipses accurately. It provides insights into the geometric properties of the curve, its shape, and its behavior in various applications.
Co-vertices
In the study of ellipses, co-vertices hold significance in determining the overall shape and orientation of the curve, thus playing a vital role in the process of finding the foci. Co-vertices are the endpoints of the minor axis, which is perpendicular to the major axis and passes through the center of the ellipse.
The connection between co-vertices and foci lies in their relationship with the semi-minor axis, denoted as ‘b’. The distance between each co-vertex and the center is equal to ‘b’. This value, along with the semi-major axis ‘a’, is crucial in calculating the distance between the foci (2c) and the eccentricity of the ellipse.
Understanding the relationship between co-vertices and foci is essential for accurate graphing and analysis of ellipses. It provides insights into the geometric properties of the curve, including its shape, size, and orientation. This understanding finds practical applications in various fields, such as architecture, engineering, and physics, where the precise determination of focal points is crucial for designing and analyzing systems.
Table: Co-vertices and Foci
| Property | Co-vertices | Foci |
|---|---|---|
| Definition | Endpoints of the minor axis, equidistant from the center | Two fixed points on the major axis, determining the shape of the ellipse |
| Distance from center | b (semi-minor axis) | c (related to ‘a’ and ‘b’) |
| Role in ellipse | Determine minor axis length and orientation | Determine shape and eccentricity |
Foci
In the study of ellipses, foci play a central role in defining the shape and properties of the curve. Understanding the connection between foci and the process of finding the focus of an ellipse is crucial for accurate analysis and applications.
- Determining the Major Axis: The foci lie on the major axis of the ellipse, which is the longest diameter passing through the center. The distance between the foci determines the length of the major axis (2a).
- Eccentricity and Shape: The eccentricity of an ellipse, a measure of its deviation from a circle, is directly related to the distance between the foci and the center. The closer the foci are to the center, the more elongated the ellipse becomes.
- Graphical Representation: When graphing an ellipse, the foci are plotted as two distinct points on the major axis, providing a visual representation of the curve’s shape and orientation.
- Applications in Design and Engineering: The precise determination of foci is essential in various fields, such as architecture and engineering. In designing elliptical structures or analyzing systems involving elliptical components, knowing the location of the foci is crucial for structural integrity and performance.
In summary, the foci of an ellipse are not just fixed points on the major axis but also key factors in determining the shape, eccentricity, and graphical representation of the curve. Understanding the connection between foci and the process of finding the focus of an ellipse is essential for accurate analysis, design, and applications in various disciplines.
Eccentricity
Eccentricity is a crucial concept in understanding the shape and properties of an ellipse. It plays a significant role in determining the location of the foci and, consequently, the overall characteristics of the ellipse. The connection between eccentricity and finding the focus of an ellipse is multifaceted and essential for accurate analysis and applications.
Eccentricity is defined as the ratio of the distance between the foci (2c) to the length of the major axis (2a). It serves as a measure of how much an ellipse deviates from a circle. A circle has an eccentricity of 0, indicating that the foci coincide with the center. As the eccentricity increases, the ellipse becomes more elongated, and the foci move away from the center.
The eccentricity of an ellipse has practical significance in various fields, including engineering, architecture, and astronomy. For instance, in orbital mechanics, the eccentricity of a planet’s orbit determines the shape of its path around the sun. A planet with a highly elliptical orbit will have a more elongated path compared to a planet with a nearly circular orbit.
In summary, understanding the connection between eccentricity and finding the focus of an ellipse is crucial for analyzing the shape and behavior of ellipses. It provides valuable insights into the geometric properties of ellipses and has practical applications in diverse fields.
Table: Eccentricity and Ellipse Characteristics
| Eccentricity | Ellipse Characteristics |
|---|---|
| 0 | Circle |
| 0 < e < 1 | Ellipse |
| e = 1 | Parabola |
Semi-major axis
In the study of ellipses, the semi-major axis plays a vital role in determining the size, shape, and geometric properties of the curve. Understanding its connection to finding the focus of an ellipse is essential for accurate analysis and applications.
- Defining the Major Axis: The major axis of an ellipse is its longest diameter, passing through the center and connecting the two vertices. The semi-major axis, denoted as ‘a’, represents half the length of this major axis.
- Relationship with Foci: The foci of an ellipse are two fixed points on the major axis, equidistant from the center. The distance between each focus and the center is related to the semi-major axis and the eccentricity of the ellipse.
- Eccentricity and Shape: The eccentricity of an ellipse measures its deviation from a circle, ranging from 0 to 1. The semi-major axis, along with the semi-minor axis, determines the eccentricity, which influences the shape of the ellipse.
- Applications in Physics and Engineering: The semi-major axis finds practical applications in various fields. For instance, in orbital mechanics, it is used to calculate the period of an orbiting body based on its distance from the central body.
In summary, the semi-major axis is a fundamental parameter in understanding the geometry and behavior of ellipses. Its connection to finding the focus of an ellipse provides valuable insights into the shape, size, and eccentricity of the curve, making it essential for various applications in physics, engineering, and other disciplines.
Semi-minor axis
In the study of ellipses, the semi-minor axis plays a significant role in determining the size, shape, and geometric properties of the curve. Understanding its connection to finding the focus of an ellipse is essential for accurate analysis and applications.
- Relationship with Foci: The foci of an ellipse are two fixed points on the major axis, equidistant from the center. The distance between each focus and the center is related to the semi-major axis ‘a’ and the semi-minor axis ‘b’ through the equation c^2 = a^2 – b^2, where ‘c’ represents the distance from the center to either focus.
- Eccentricity and Shape: The eccentricity of an ellipse measures its deviation from a circle, ranging from 0 to 1. The semi-major axis ‘a’ and the semi-minor axis ‘b’ determine the eccentricity, which influences the shape of the ellipse. A larger difference between ‘a’ and ‘b’ results in a more elongated ellipse.
- Applications in Engineering and Architecture: The semi-minor axis finds practical applications in various fields. For instance, in architecture, it is used to calculate the dimensions of elliptical arches and domes, ensuring structural stability and aesthetic appeal.
- Connection to Area and Perimeter: The semi-major axis ‘a’ and the semi-minor axis ‘b’ are used to calculate the area and perimeter of an ellipse. These calculations are essential in fields such as surveying, land measurement, and resource allocation.
In summary, the semi-minor axis ‘b’ is a fundamental parameter in understanding the geometry and behavior of ellipses. Its connection to finding the focus of an ellipse, along with its role in determining the eccentricity, shape, and various applications, makes it an essential concept in the study of conic sections.
Distance between foci
Determining the distance between foci is a crucial step in understanding the geometry and behavior of ellipses. This distance, denoted as 2c, plays a significant role in finding the focus of an ellipse and provides valuable insights into the shape and properties of the curve.
- Eccentricity and Shape: The distance between foci is directly related to the eccentricity of the ellipse, which measures its deviation from a circle. A larger distance between foci corresponds to a higher eccentricity, resulting in a more elongated ellipse.
- Relationship with Semi-Major and Semi-Minor Axes: The distance between foci, along with the semi-major axis ‘a’ and the semi-minor axis ‘b’, determines the overall shape and size of the ellipse. These parameters are used to calculate the area and perimeter of the ellipse.
- Applications in Physics and Engineering: The distance between foci finds practical applications in various fields. For instance, in orbital mechanics, it is used to calculate the eccentricity of planetary orbits, which influences the shape and duration of their paths around the sun.
In summary, understanding the distance between foci is essential for accurately finding the focus of an ellipse. This distance provides insights into the shape, eccentricity, and various applications of ellipses in scientific and engineering disciplines.
Frequently Asked Questions (FAQs) on Finding the Focus of an Ellipse
This section aims to address common questions and misconceptions regarding the process of finding the focus of an ellipse. Each question and answer is carefully crafted to provide clear and informative explanations.
Question 1: What is the significance of finding the focus of an ellipse?
Finding the focus of an ellipse is essential for understanding the geometric properties of the curve. It provides insights into the shape, eccentricity, and behavior of the ellipse, which are crucial for various applications in mathematics, physics, engineering, and other fields.
Question 2: How does the focus affect the shape of an ellipse?
The distance between the foci determines the eccentricity of the ellipse, which measures its deviation from a circle. A larger distance between foci corresponds to a higher eccentricity, resulting in a more elongated ellipse.
Question 3: What is the relationship between the focus and the center of an ellipse?
The foci of an ellipse are located on the major axis, equidistant from the center. The distance between the center and each focus is related to the lengths of the semi-major and semi-minor axes.
Question 4: How can I find the focus of an ellipse given its equation?
To find the focus of an ellipse given its equation, you can use the standard equation of an ellipse and apply the appropriate formula. The formula for finding the coordinates of the foci depends on the orientation of the ellipse (horizontal or vertical).
Question 5: Why is it important to understand the concept of finding the focus of an ellipse?
Understanding how to find the focus of an ellipse is important for analyzing and solving problems involving ellipses. It enables professionals in various fields to accurately determine the properties and behavior of elliptical curves, which have applications in areas such as orbital mechanics, acoustics, and architectural design.
Question 6: Are there any online resources or tools that can help me find the focus of an ellipse?
Yes, there are several online resources and tools available that can assist you in finding the focus of an ellipse. These resources can provide step-by-step guidance, interactive simulations, and calculators to simplify the process.
In summary, understanding how to find the focus of an ellipse is essential for analyzing the geometric properties and behavior of ellipses. The FAQs addressed in this section provide clear and informative explanations to common questions, empowering readers with the knowledge to solve problems and apply this concept in various disciplines.
Transition to the next article section:
To delve deeper into the topic, the following section will explore advanced techniques and applications of finding the focus of an ellipse.
Tips on Finding the Focus of an Ellipse
To effectively find the focus of an ellipse, consider the following tips:
Utilize the Center and Vertices: Identify the center and vertices of the ellipse. The center is the midpoint of the major axis, and the vertices are the endpoints. Knowing these points aids in determining the focus.
Employ the Standard Equation: If given the equation of the ellipse, use the standard equation to determine the lengths of the semi-major and semi-minor axes. These values are crucial for calculating the focus.
Apply the Distance Formula: Use the distance formula to calculate the distance between the center and each vertex. This distance is equal to the semi-major axis length.
Determine the Eccentricity:
Calculate the eccentricity of the ellipse using the formula: Eccentricity = sqrt((a^2 – b^2) / a^2), where ‘a’ is the semi-major axis length and ‘b’ is the semi-minor axis length.
Calculate the Distance to Focus:
Multiply the eccentricity by the semi-major axis length to find the distance from the center to each focus.
Locate the Foci:
The foci lie on the major axis, equidistant from the center. Use the calculated distance to determine the exact location of the foci.
By following these tips, you can accurately find the focus of an ellipse, providing valuable insights into its geometric properties and behavior.
Transition to the article’s conclusion:
In conclusion, understanding how to find the focus of an ellipse is essential for analyzing and solving problems involving elliptical curves. By applying these practical tips, you can effectively determine the focal points of ellipses, empowering you to solve complex problems and gain a deeper understanding of this important conic section.
Conclusion
This comprehensive guide has explored the intricacies of finding the focus of an ellipse, a fundamental concept in the study of conic sections. By understanding the techniques and applications outlined in this article, individuals can effectively analyze and solve problems involving elliptical curves.
The focus of an ellipse plays a vital role in determining the shape, eccentricity, and behavior of the curve. Through the process of finding the focus, we gain valuable insights into the geometric properties of ellipses, enabling us to apply this knowledge in diverse fields such as mathematics, physics, engineering, and architecture.
In conclusion, mastering the skill of finding the focus of an ellipse empowers us to accurately analyze and solve complex problems involving elliptical curves. By embracing the techniques and tips presented in this article, individuals can unlock the potential of this important mathematical concept and contribute to advancements in various disciplines.
Youtube Video:
