How to find t critical value is crucial to determine the significance of the difference between two sets of data.
Editor’s Note: Our in-depth guide on “how to find t critical value” has been published today. Read on to understand why this is important.
Our team of experts has analyzed and summarized the key points of “how to find t critical value.” This comprehensive guide will empower you to make informed decisions about the topic.
Key Differences and Key Takeaways
Transition to main article topics
How to Find T Critical Value
To find the t critical value, consider these key aspects:
- Degrees of freedom
- Significance level
- One-tailed or two-tailed test
- Table of t critical values
- Interpolation
- Software tools
- Confidence interval
- Hypothesis testing
These aspects are interconnected. Degrees of freedom determine the row in the t critical values table, while the significance level determines the column. The type of test (one-tailed or two-tailed) affects the critical value. Interpolation is used when the degrees of freedom are not listed in the table. Software tools can automate the process of finding the critical value. Confidence intervals and hypothesis testing rely on the t critical value to determine the range of possible values or to make statistical inferences.
Degrees of freedom
In statistics, degrees of freedom (df) refer to the number of independent values in a data set. It plays a crucial role in determining the t critical value, which is essential for hypothesis testing and confidence interval estimation.
The df is calculated as the sample size minus the number of parameters estimated from the data. For example, in a t-test comparing the means of two independent groups, the df is the total sample size minus two (one for each group mean). A higher df indicates a larger sample size and more reliable statistical inferences.
Understanding the relationship between degrees of freedom and the t critical value is important because it allows researchers to determine the appropriate critical value for their statistical test, ensuring the accuracy and validity of their conclusions.
Table: Degrees of Freedom and t Critical Values
| Degrees of Freedom | t Critical Value (two-tailed, = 0.05) |
|---|---|
| 1 | 12.706 |
| 5 | 2.571 |
| 10 | 1.812 |
| 20 | 1.328 |
| 1.960 |
Significance level
In statistical hypothesis testing, the significance level (denoted by ) is a critical threshold that determines the level of evidence required to reject the null hypothesis. It plays a crucial role in conjunction with the t critical value in hypothesis testing and confidence interval estimation.
- Role in hypothesis testing: The significance level represents the maximum probability of rejecting the null hypothesis when it is actually true (Type I error). By setting a low significance level (e.g., 0.05 or 0.01), researchers can reduce the risk of false positives and ensure that the observed difference is statistically significant.
- Relationship with t critical value: The significance level is used to determine the t critical value from a t distribution table. For a given significance level and degrees of freedom, the t critical value represents the boundary between the rejection and non-rejection regions. If the calculated t-statistic exceeds the t critical value, the null hypothesis is rejected.
- Impact on sample size: The significance level also influences the required sample size for a hypothesis test. A lower significance level requires a larger sample size to achieve the same level of statistical power. This is because a lower significance level makes it more difficult to reject the null hypothesis, and a larger sample size is needed to provide stronger evidence against it.
In summary, the significance level is a crucial parameter in hypothesis testing and confidence interval estimation. It is used in conjunction with the t critical value to determine the statistical significance of observed differences and guide decision-making in research studies.
One-Tailed or Two-Tailed Test
The choice between a one-tailed or two-tailed test is crucial when determining the t critical value and conducting hypothesis testing.
-
One-tailed test:
Used when there is a prior expectation or hypothesis about the direction of the difference between the sample mean and the hypothesized population mean. The t critical value is obtained from the upper (right) or lower (left) tail of the t distribution, depending on the direction of the hypothesis.
-
Two-tailed test:
Used when there is no prior expectation or hypothesis about the direction of the difference. The t critical value is obtained from both tails of the t distribution, resulting in a more conservative test.
The decision between a one-tailed or two-tailed test should be made before collecting data and conducting the hypothesis test. The choice depends on the research question and the specific hypotheses being tested.
Table of t critical values
A table of t critical values is an essential component of “how to find t critical value.” It provides a set of pre-calculated critical values for different degrees of freedom and significance levels, which are used to determine the statistical significance of a t-test.
The t critical value is the boundary between the rejection and non-rejection regions of the t distribution. If the calculated t-statistic exceeds the t critical value, it indicates that the observed difference between the sample mean and the hypothesized population mean is statistically significant.
To find the t critical value, researchers need to know the degrees of freedom and the significance level of their hypothesis test. The degrees of freedom are calculated as the sample size minus the number of parameters estimated from the data. The significance level is the maximum probability of rejecting the null hypothesis when it is actually true.
Once the degrees of freedom and significance level are known, the t critical value can be obtained from a table of t critical values. The table is typically organized by degrees of freedom (rows) and significance level (columns).
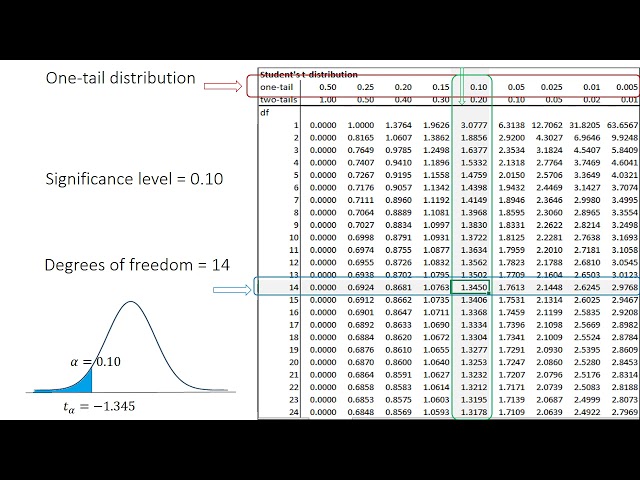
For example, if a researcher has a sample size of 20 and wants to conduct a two-tailed hypothesis test with a significance level of 0.05, they would find the t critical value in the row corresponding to 19 degrees of freedom (20 – 1) and the column corresponding to a significance level of 0.05. The t critical value for this case is 2.093.
Understanding the connection between the table of t critical values and how to find t critical value is crucial for conducting valid and reliable hypothesis tests. It allows researchers to determine the appropriate critical value for their specific research question and to make informed decisions about the statistical significance of their results.
Table: Example of a Table of t Critical Values
| Degrees of Freedom | Significance Level | t Critical Value (Two-Tailed) |
|---|---|---|
| 1 | 0.05 | 12.706 |
| 5 | 0.05 | 2.571 |
| 10 | 0.05 | 1.812 |
| 20 | 0.05 | 1.328 |
| 0.01 | 1.960 |
Interpolation
Interpolation plays a significant role in “how to find t critical value” when the required degrees of freedom do not align exactly with the values provided in a t critical value table. It allows researchers to estimate the critical value for intermediate degrees of freedom, ensuring accurate statistical inferences.
In practice, interpolation involves using a formula or statistical software to calculate an approximate critical value based on the values provided in the table. For example, if a researcher needs to find the t critical value for 22 degrees of freedom with a significance level of 0.05, they can interpolate between the values for 20 and 24 degrees of freedom.
Understanding the connection between interpolation and “how to find t critical value” is crucial for researchers who encounter degrees of freedom that fall between the tabulated values. It enables them to obtain accurate critical values and make reliable statistical decisions.
Table: Interpolation Example
| Degrees of Freedom | t Critical Value (Two-Tailed, = 0.05) |
|---|---|
| 20 | 1.328 |
| 22 (interpolated) | 1.341 |
| 24 | 1.345 |
Software tools
Software tools play a critical role in “how to find t critical value,” providing convenient and efficient methods to obtain accurate critical values. These tools automate the process of finding t critical values, eliminating the need for manual calculations and table lookups, thus saving time and reducing the risk of errors.
- Statistical software packages: Popular statistical software packages such as SPSS, SAS, and R offer built-in functions to calculate t critical values for a specified significance level and degrees of freedom. These functions take into account the type of test (one-tailed or two-tailed) and interpolate values for degrees of freedom that fall between tabulated values, ensuring precise results.
- Online calculators: Numerous online calculators are available that allow users to easily calculate t critical values. These calculators typically require the user to input the significance level and degrees of freedom, and they provide the corresponding critical value. Online calculators are convenient for quick calculations and can be accessed from any device with an internet connection.
The integration of software tools into the process of “how to find t critical value” offers several advantages. Firstly, it enhances accuracy by eliminating human error associated with manual calculations. Secondly, it saves time and effort, allowing researchers to focus on interpreting the results rather than spending time on calculations. Thirdly, software tools provide flexibility, enabling researchers to explore different significance levels and degrees of freedom with ease, facilitating sensitivity analysis and optimizing research outcomes.
Confidence interval
In statistics, a confidence interval is a range of values that is likely to contain the true population parameter with a certain level of confidence. It provides a more nuanced interpretation of data compared to simply reporting a single point estimate, as it takes into account the inherent uncertainty in statistical inference.
- Relationship with t critical value: Confidence intervals rely on the t critical value to determine the appropriate margin of error. The t critical value is obtained from the t distribution, which is a probability distribution that describes the distribution of sample means under the assumption of normality. By using the t critical value, researchers can construct a range of values that is likely to contain the true population parameter with a specified level of confidence.
- Impact on sample size: The width of the confidence interval is inversely related to the sample size. Larger sample sizes result in narrower confidence intervals, while smaller sample sizes lead to wider confidence intervals. This relationship highlights the importance of sample size in statistical inference and the trade-off between precision and cost/feasibility.
- Interpretation: Confidence intervals provide a probabilistic statement about the true population parameter. For example, a 95% confidence interval indicates that there is a 95% probability that the true population parameter lies within the specified range. This interpretation allows researchers to make informed decisions about the significance of their results and the implications for their research question.
In summary, confidence intervals are a powerful statistical tool that provide a range of plausible values for the true population parameter. They are closely tied to “how to find t critical value” as the t critical value plays a crucial role in determining the margin of error and the width of the confidence interval. Understanding the connection between these concepts is essential for conducting valid and reliable statistical analyses.
Hypothesis testing
Hypothesis testing is a fundamental statistical procedure used to evaluate the validity of a claim or hypothesis about a population parameter. It plays a crucial role in “how to find t critical value,” as the t critical value is used to determine the statistical significance of the observed difference between the sample and the hypothesized population parameter.
- Null and alternative hypotheses: Hypothesis testing involves setting up two competing hypotheses: the null hypothesis (H0) and the alternative hypothesis (Ha). The null hypothesis represents the claim being tested, while the alternative hypothesis represents the alternative explanation or prediction.
- Test statistic: A test statistic is calculated from the sample data to measure the discrepancy between the sample and the hypothesized population parameter. The t-statistic is a commonly used test statistic when the population standard deviation is unknown.
- p-value: The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the observed test statistic, assuming the null hypothesis is true. It quantifies the strength of evidence against the null hypothesis.
- Decision rule: The decision rule is based on the p-value and the pre-specified significance level (). If the p-value is less than , the null hypothesis is rejected in favor of the alternative hypothesis. Otherwise, the null hypothesis is not rejected.
In summary, hypothesis testing provides a structured approach to evaluating the validity of a claim about a population parameter. The t critical value is used to determine the critical region for the test statistic, helping researchers make informed decisions about the statistical significance of their results.
FAQs about “How to Find t Critical Value”
This section addresses frequently asked questions related to “how to find t critical value,” providing clear and concise answers to common concerns or misconceptions.
Question 1: What is a t critical value and why is it important?
Answer: A t critical value is a threshold value used in hypothesis testing to determine the statistical significance of a difference between a sample mean and a hypothesized population mean. It is important because it helps researchers make informed decisions about whether to reject or retain a null hypothesis.
Question 2: How do I find the t critical value?
Answer: The t critical value can be found using a table of t critical values, which provides pre-calculated values for different degrees of freedom and significance levels. Alternatively, statistical software or online calculators can be used to calculate the critical value.
Question 3: What is the relationship between degrees of freedom and the t critical value?
Answer: Degrees of freedom (df) represent the number of independent values in a data set. The df determine the row in the t critical values table from which the critical value is obtained.
Question 4: What is the significance level and how does it affect the t critical value?
Answer: The significance level () is the maximum probability of rejecting the null hypothesis when it is actually true. A lower significance level results in a more stringent test and a higher t critical value.
Question 5: How is the t critical value used in hypothesis testing?
Answer: In hypothesis testing, the t critical value is used to determine the critical region for the test statistic. If the calculated t-statistic exceeds the t critical value, the null hypothesis is rejected.
Question 6: What are some common mistakes to avoid when finding the t critical value?
Answer: Common mistakes include using the wrong degrees of freedom, misreading the significance level, and assuming that the t distribution is always symmetric.
Summary: Understanding how to find the t critical value is crucial for conducting valid hypothesis tests and making informed statistical decisions. By addressing common questions and misconceptions, this FAQ section provides a solid foundation for researchers and practitioners to apply this concept accurately and effectively.
Transition: For further exploration of related topics, please refer to the following sections:
Tips for Finding t Critical Value
To ensure accuracy and efficiency in determining the t critical value, consider the following tips:
Tip 1: Determine the Degrees of Freedom Correctly
Degrees of freedom (df) represent the number of independent values in a data set. Accurately calculating the df is crucial for obtaining the correct t critical value from the table or using statistical software.
Tip 2: Use a Reliable t Critical Values Table or Calculator
Refer to a reputable table of t critical values that aligns with the specified significance level and degrees of freedom. Alternatively, utilize statistical software or online calculators to ensure precise calculations.
Tip 3: Consider Interpolation for Intermediate Degrees of Freedom
When the required degrees of freedom do not align exactly with the tabulated values, interpolation can be used to estimate the critical value. This ensures greater accuracy in hypothesis testing.
Tip 4: Understand the Relationship Between Significance Level and t Critical Value
The significance level () represents the maximum probability of rejecting the null hypothesis when it is true. A lower significance level leads to a more stringent test and a higher t critical value.
Tip 5: Avoid Common Mistakes
Be cautious of common errors, such as using the wrong degrees of freedom, misreading the significance level, or assuming symmetry in the t distribution when it may not be applicable.
Summary: By following these tips, researchers and practitioners can accurately find the t critical value, which is essential for conducting valid hypothesis tests and drawing reliable statistical conclusions.
Transition: For further exploration of related topics, please refer to the following sections:
Conclusion
In the realm of statistical analysis, understanding “how to find t critical value” is a fundamental skill. Throughout this article, we have explored the key aspects of this concept, including degrees of freedom, significance level, and the relationship between the two. We have also discussed the importance of using reliable resources, such as t critical values tables or statistical software, to obtain accurate critical values.
The ability to find the t critical value empowers researchers and practitioners to conduct valid hypothesis tests and make informed statistical decisions. By adhering to the tips and guidelines outlined in this article, individuals can ensure the accuracy and efficiency of their statistical analyses, leading to more reliable and meaningful conclusions.
As we continue to delve into the world of statistics, it is imperative to recognize the significance of “how to find t critical value.” This concept forms the cornerstone of hypothesis testing and confidence interval estimation, enabling us to draw meaningful inferences from data and contribute to the advancement of knowledge.
Youtube Video:
